(Inceptionv3) Rethinking the Inception Architecture for Computer Vision
출처: https://arxiv.org/abs/1512.00567
요약 및 방법론
핵심 아이디어
계산 효율성과 적은 파라미터 수는 모바일 비전, 빅데이터 등 다양한 활용 사례에서 중요하다. 본 논문은 적절한 합성곱 분해와 강력한 정규화를 통해 추가 계산을 효율적으로 활용하는 네트워크 확장 방법을 제안한다. ILSVRC 2012 분류 챌린지 검증 세트에서 단일 프레임 평가 기준 5B(50억) multiply-add 연산량, 2,500만 미만 파라미터로 Top-1 오류율 21.2%, Top-5 오류율 5.6%를 달성했다. 4개 모델 앙상블과 multi-crop 평가에서는 Top-1 오류율 17.2%(초록 17.3%), Top-5 오류율 3.58%(초록 3.5%)를 기록했다. (초록 수치는 반올림, 표 수치는 정밀 표기)
주요 내용 요약
- 계산 효율성과 적은 파라미터로 모바일 등 다양한 환경에 적합
- 합성곱 분해(Factorized Convolutions), 정규화(Regularization), 효율적 grid 축소, 보조 분류기의 정규화 역할, 라벨 스무딩(Label Smoothing), 학습 세팅(RMSProp, gradient clipping 등), 저해상도 입력 실험이 핵심
주요 성과
- 단일 crop(Inception-v3): Top-1 21.2%, Top-5 5.6%
- 단일 모델·멀티 crop(144): Top-1 18.77%, Top-5 4.2%
- 앙상블(4모델·144 crop): Top-1 17.2%(초록 17.3%), Top-5 3.58%(초록 3.5%)
의의
- 효율적 아키텍처 설계의 중요성 입증, 이후 MobileNet, EfficientNet 등으로 발전
서론 및 결론 요약
서론
2012년 ImageNet 대회 이후, 깊고 넓은 합성곱 신경망이 컴퓨터 비전 성능을 크게 끌어올렸다. VGGNet은 단순하지만 계산 비용이 매우 크고, GoogLeNet(Inception)은 메모리·연산 자원 제약이 엄격한 상황에서도 좋은 성능을 낸다(GoogLeNet: 5M 파라미터, VGGNet: 60M 파라미터). 하지만 Inception 구조는 복잡해 단순 확장이 어렵고, 필터 수만 늘리면 연산량·파라미터 수가 급격히 증가한다. 본 논문은 효율적 확장을 위한 일반 원칙과 최적화 아이디어를 제시한다.
결론
Inception-v3는 상대적으로 낮은 계산 비용으로 높은 성능을 달성했다(단일 crop 기준 Top-1 21.2%, Top-5 5.6%). 4개 모델 앙상블·multi-crop에서는 Top-1 17.2%(초록 17.3%), Top-5 3.58%(초록 3.5%)로, 기존 최고 성과 대비 25% 이상 개선되었다. 입력 해상도가 낮아도(79×79) 높은 성능을 유지할 수 있음을 보였고, 합성곱 분해와 차원 축소, 보조 분류기(BN 적용), 라벨 스무딩 등으로 작은 데이터셋에서도 고성능 학습이 가능함을 입증했다.
핵심 기여 요인: 합성곱 분해, Grid Reduction, Label Smoothing, Auxiliary Classifier(보조 분류기)
일반 설계 원칙
- 표현 병목을 피하라: 네트워크 초반부에서 지나친 압축은 성능에 악영향을 준다. 표현 크기는 점진적으로 줄어들어야 하며, 차원 수는 정보량의 대략적 추정치일 뿐이다.
- 고차원 표현은 지역적으로 처리하기 쉽다: 활성화 채널(타일)이 많을수록 특징이 더 빨리 분리되고 학습 속도가 빨라진다.
- 공간적 집계는 저차원 임베딩에서도 큰 손실 없이 가능: 인접 유닛 간 상관관계가 높아 차원 축소 후에도 정보 손실이 적다.
- 폭과 깊이의 균형: 동일 연산량 내에서 깊이와 폭을 균형 있게 늘릴 때 최적 성능을 얻는다.
핵심 메시지: 단순히 네트워크를 크게 만드는 대신, 정보 흐름을 막지 않고 효율적으로 차원을 다루며, 폭과 깊이를 균형 있게 설계해야 한다.
합성곱 분해와 효율화
5×5 합성곱 분해: 5×5 합성곱은 동일 조건의 3×3 합성곱보다 약 2.78배 연산이 크다. 5×5를 3×3 두 층으로 대체하면 인접 타일 간 계산 재사용으로 연산이 (9+9)/25 ≈ 0.72배로 줄어 약 28% 절감된다.
3×3 비대칭 분해: 3×3 합성곱을 3×1, 1×3 두 층으로 분해하면 연산량이 33% 절감된다. 2×2 두 겹 분해는 11% 절감에 그친다. n×n 합성곱을 1×n, n×1로 분해할수록 절감 효과가 커진다(중간 feature map에서 효과적).
보조 분류기: 초기 수렴 개선이 아니라 정규화 효과가 핵심이다. 보조 분류기에 BN/Dropout을 적용하면 주 분류기의 성능이 향상된다.
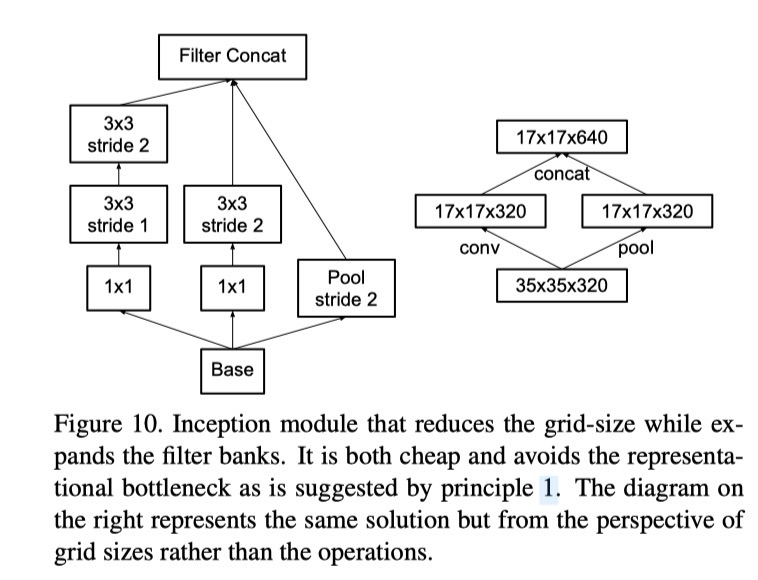
Efficient grid reduction: stride-2 풀링과 stride-2 합성곱을 병렬로 두고 concat하는 설계로 병목을 피하면서 연산 효율도 확보한다.
| 라벨 스무딩(Label Smoothing): q′(k | x) = (1−ε)δ_k,y + ε·u(k) (u(k): 균등분포)로, ε=0.1에서 Top-1/Top-5 오류율이 약 0.2% 절감된다. |
저해상도 입력 실험: 79/151/299 해상도 실험에서 연산량을 맞추면 최종 품질 차이가 크지 않다. 작은 객체 탐지에 저해상도 전용 네트워크 활용 가능성을 시사한다.
학습 세팅: TensorFlow 분산 학습, 50개 Nvidia Kepler GPU, batch size 32, 100 epoch, RMSProp(최적), learning rate decay, gradient clipping(2.0), 파라미터 이동 평균(running average) 등 안정화 기법을 결합.
10장 요약 및 누적 변경 효과
누적 변경을 단계적으로 적용할수록 성능이 향상된다. Inception-v2(기본) → +RMSProp → +Label Smoothing → +Factorized 7×7 → +BN-auxiliary(최종 Inception-v3). 최종 단일 crop 성능은 Top-1 21.2%, Top-5 5.6%. 단일 모델·멀티 crop(144)에서 Top-1 18.77%, Top-5 4.2%. 4모델 앙상블·멀티 crop(144)에서 Top-1 17.2%(초록 17.3%), Top-5 3.58%(초록 3.5%).
그림/표/캡션
이미지, 표 등은 원문 그림/표 캡션을 그대로 옮겨 번역(이미지 자체는 생략)
예시: 그림 1: 5×5 합성곱의 계산 그래프 구조. 그림 2: 선형/비선형 활성화 실험 결과. 표 1: 제안 네트워크 아키텍처 개요. 표 2: 입력 해상도별 성능 비교 등.
오탈자 및 용어 교정
- Nvidia(정확 표기)
- classifier(분류기) 등 약어 풀어쓰기
출처
https://arxiv.org/abs/1512.00567
내용
- 표현 병목을 피하라(Avoid representational bottleneck) : 네트워크 초반부에서, 순방향 전파는 입력층에서부터 분류기나 회귀기로 이어지는 비순환 그래프로 표현될 수 있으며 이는 명확한 정보의 흐름을 제공한다. 이때 입력과 출력을 구분하는 임의의 절단면을 고려할때, 그 지점을 통과하는 정보량을 측정할 수 있는데, 지나친 압축을 통한 병목을 피해야한다.
- 일반적으로 점진적으로 줄어들어야 한다.
- 이론적으로 정보량은 단순히 차원수로는 표현 할 수 없는데, 이는 상관을 고려해야하기 때문이다. 즉 차원수는 대략적인 추정치만 제공한다.
- 즉 초기층의 지나친 압축은 성능에 악영향
- 고차원 표현은 network에서 지역적으로 처리하기 더 쉽다. 더 많은 활성화채널(타일)은 더 많은 분리된 특징을 얻을 수 있다. 이는 네트워크가 더 빠르게 학습되도록 한다.
- 차원을 높이면, 특징이 더 빨리 분리되며 이를 통해 학습속도가 빨라진다.
- 공간적 집계(spatial aggregation)는 저차원 임베딩에서도 큰 손실 없이 수행될 수 있다. 공간 연산을 수행하기 전 입력 표현의 차원을 줄여도 심각한 부작용이 발생하지 않는다. 이는 인접 유닛간 강력한 상관관계 때문이며, 덕분에 차원 축소시 정보 손실이 적다. 이러한 방식으로 신호를 압축시킴으로서, 오히려 학습을 빠르게 만들 수 있다.
- 인접 픽셀간 상관관계가 높기 때문에, 차원축소를 통한 압축을 먼저 해도 정보 손실이 크지 않다.
- 네트워크의 폭(width)과 깊이(depth)를 균형 있게 조절. 최적의 성능은 적절한 깊이의 네트워크가 필요하며, 필터의 크기를 높이면 네트워크의 품질을 높일 수 있다. 다만 동일한 연산량 내에서의 최적 성능 향상은 적절한 폭과 깊이의 균형점에서 일어난다.
- 깊이, 폭을 균형있게 조절해야한다.(서로 하나씩만 늘리는것보다 균형있게 늘리는게 좋음)
포인트
| 항목 | 내용 |
|---|---|
| 병목 회피 | 초기 층에서 지나친 압축을 피해야 함 |
| 고차원 표현 | 더 많은 활성화 채널 → 더 분리된 특징, 학습 가속 |
| 차원 축소 | 3×3 같은 큰 합성곱 전에는 채널 수 축소 가능 (정보 손실 적음) |
| 폭·깊이 균형 | 연산 예산 내에서 깊이와 폭을 동시에 늘릴 때 최적 성능 |
핵심 메시지: 단순히 네트워크를 크게 만드는 대신, 정보 흐름을 막지 않고 효율적으로 차원을 다루며, 폭과 깊이를 균형 있게 설계해야 한다
📚 3. Factorizing Convolutions with Large Filter Size
번역
큰 필터 크기를 갖는 합성곱의 분해 GoogLeNet 네트워크의 초기 성능 향상 대부분은 차원 축소(dimension reduction)의 적극적인 활용에서 기인한다. 이는 연산 효율적인 합성곱 분해(factorizing convolutions)의 특수한 사례로 볼 수 있다. 예를 들어, 1×1 합성곱 층 뒤에 3×3 합성곱 층을 두는 경우를 생각해보자. 비전 네트워크에서는 인접한 활성화 값들이 강하게 상관되어 있다고 기대할 수 있다. 따라서 이들의 활성화를 집계(aggregation)하기 전에 차원을 줄여도 표현력 있는 로컬 표현을 얻을 수 있다.
여기서는 다양한 상황에서 합성곱을 분해하는 다른 방법들을 탐구한다. 특히, 해법의 계산 효율성을 높이는 것이 목표이다. Inception 네트워크는 완전 합성곱(fully convolutional) 구조이므로, 각 가중치는 활성화 하나당 곱셈 한 번에 해당한다. 따라서 계산 비용을 줄이면 곧바로 파라미터 수 감소로 이어진다. 즉, 적절한 분해를 적용하면 더 분리된(disentangled) 파라미터를 얻을 수 있어 학습 속도가 빨라지고, 절약된 연산/메모리 자원은 필터 뱅크 크기 확장에 활용하면서도 단일 머신에서 각 모델 복제본을 학습할 수 있게 된다.
3.1. Factorization into smaller convolutions
큰 공간 필터(예: 5×5, 7×7)를 사용하는 합성곱은 연산 비용 면에서 불균형적으로 비싸다. 예를 들어, n개의 필터를 가진 5×5 합성곱은 m개의 필터 그리드에서 동일한 필터 수를 가진 3×3 합성곱보다 연산량이 25/9 ≈ 2.78배 더 많다. 물론 5×5 필터는 더 넓은 영역의 활성화 간 신호 의존성을 포착할 수 있으므로, 필터 크기를 줄이면 표현력(expressiveness) 손실이 발생한다. 그러나 5×5 합성곱을 동일한 입력 크기와 출력 깊이를 가진 더 적은 파라미터의 다층 네트워크로 대체할 수 있는지 물어볼 수 있다.
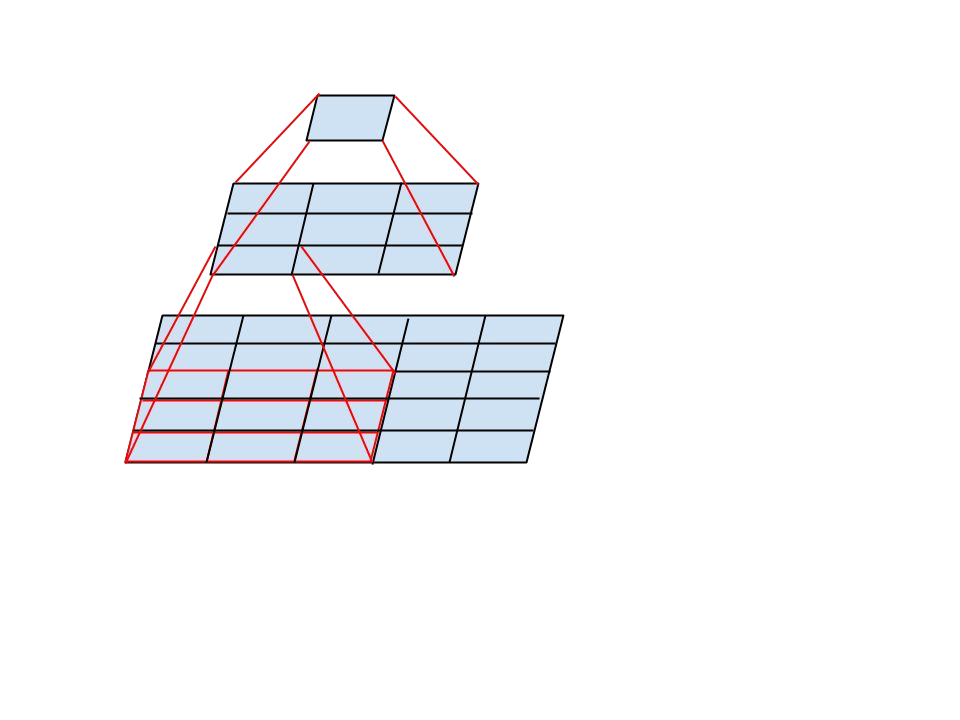
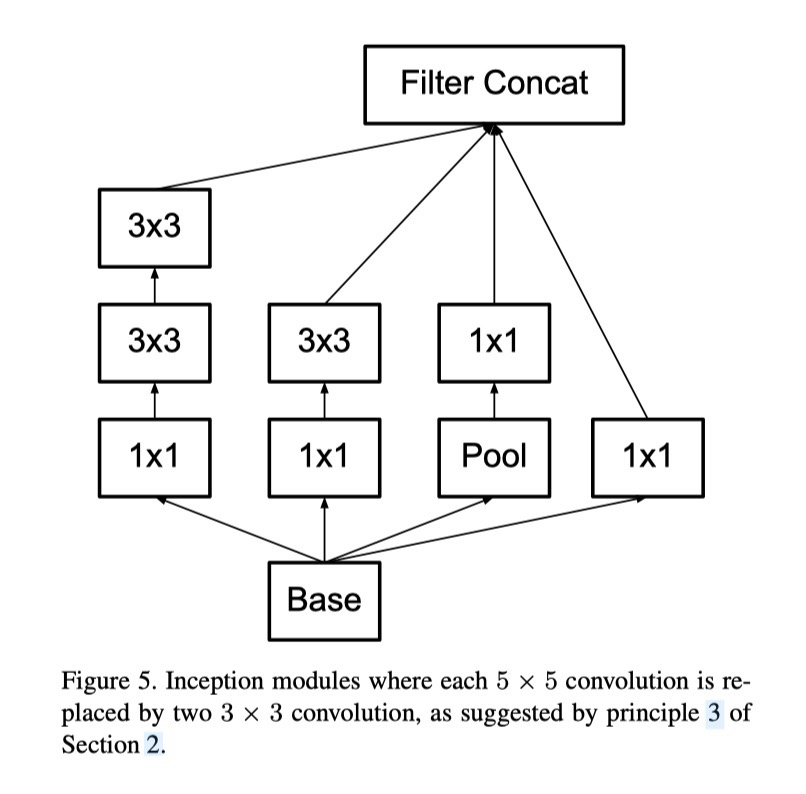
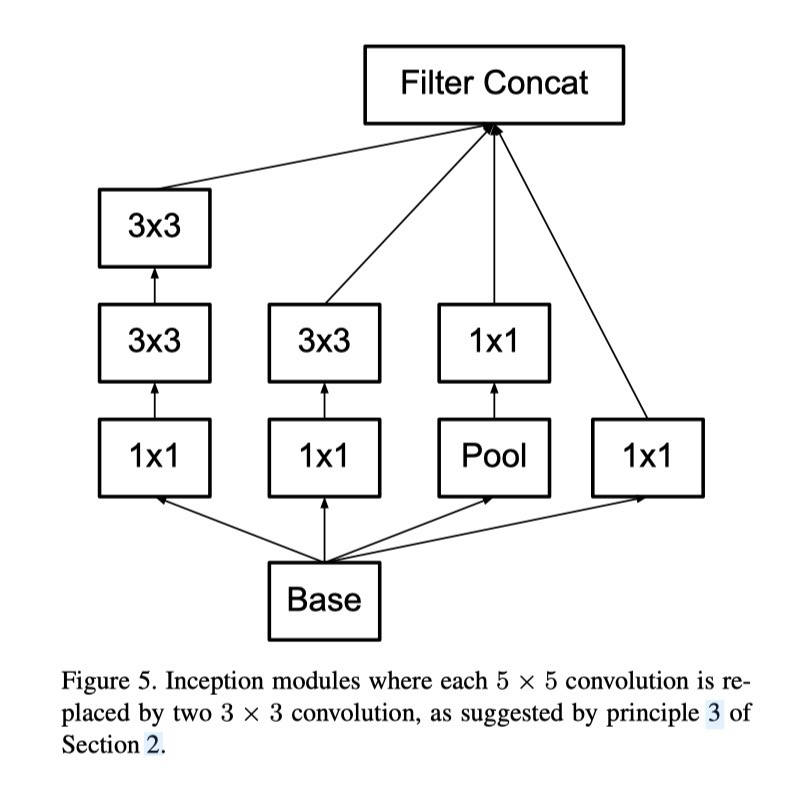
5×5 합성곱의 계산 그래프를 자세히 들여다보면, 각 출력은 입력의 5×5 타일 위를 슬라이딩하는 작은 완전 연결 네트워크(fully-connected network)와 유사하다(그림 1 참조). 비전 네트워크를 구성하는 상황에서는 다시 한 번 병진 불변성(translation invariance)을 활용하여, 완전 연결 계층을 2층 합성곱 구조로 대체하는 것이 자연스럽다: 첫 번째 층은 3×3 합성곱이고, 두 번째 층은 첫 번째 층의 3×3 출력 그리드 위에 있는 완전 연결 계층이다(그림 1). 이 작은 네트워크를 입력 활성화 그리드에 슬라이딩하는 것은 곧 5×5 합성곱을 2개의 3×3 합성곱으로 대체하는 것과 같다(그림 4와 5 비교).
이 구조는 인접 타일 간 가중치 공유 덕분에 파라미터 수를 확실히 줄인다. 계산 비용 절감을 정량적으로 분석하기 위해 몇 가지 단순화된 가정을 두자: n = αm이라고 가정하자. 즉, 활성화 수를 α배로 변환한다고 할 수 있다. 5×5 합성곱은 집계 연산이므로 α는 보통 1보다 조금 크다(GoogLeNet에서는 약 1.5). 5×5 층을 2층 구조로 대체한다면, 두 단계에서 각각 √α배만큼 필터 수를 늘리는 것이 합리적이다. 단순화를 위해 α=1이라고 두면(확장 없음), 인접 그리드 타일 간 계산을 재사용하지 않는다면 오히려 연산량이 늘어난다. 그러나 두 개의 3×3 합성곱 층으로 슬라이딩 네트워크를 표현하면 인접 타일 간 활성화를 재사용할 수 있다. 이렇게 하면 계산량은 (9+9)/25 = 18/25로 줄어들어 약 28% 절감된다. 파라미터 수 절감도 동일하다.
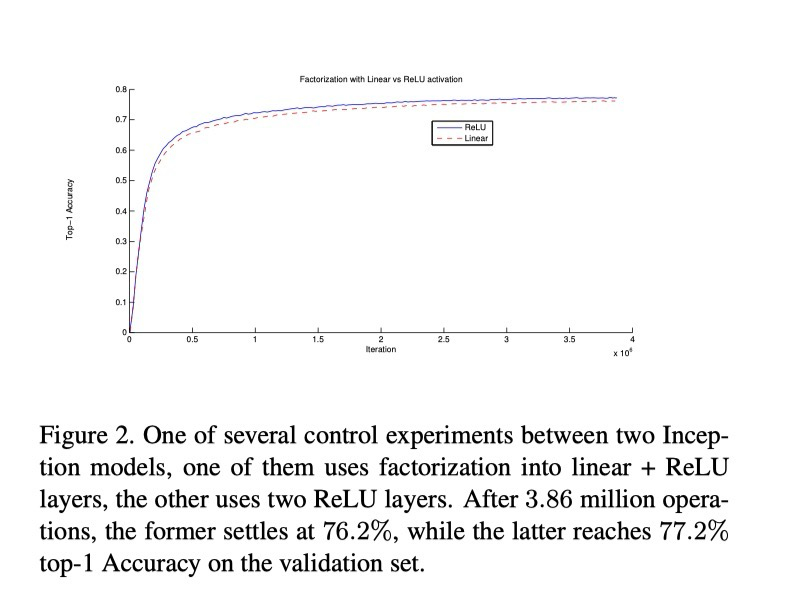
그러나 이 접근법은 두 가지 일반적인 질문을 야기한다. 첫째, 이 대체가 표현력 손실을 일으키지 않는가? 둘째, 계산의 선형 부분만 분해하는 것이 목적이라면 첫 번째 층에는 선형 활성화(linear activation)를 유지하는 것이 더 낫지 않은가? 여러 통제 실험을 수행한 결과(그림 2 참조), 선형 활성화는 항상 ReLU보다 성능이 떨어졌다. 특히 출력 활성화에 배치 정규화(batch normalization)를 적용하면 네트워크가 학습할 수 있는 표현 공간이 확장되어 이득이 커졌다. 유사한 효과는 차원 축소 모듈에서 선형 활성화를 사용할 때도 관찰된다.
3.2. Spatial Factorization into Asymmetric Convolutions
3.2. 비대칭 합성곱(Asymmetric Convolutions)을 통한 공간적 분해
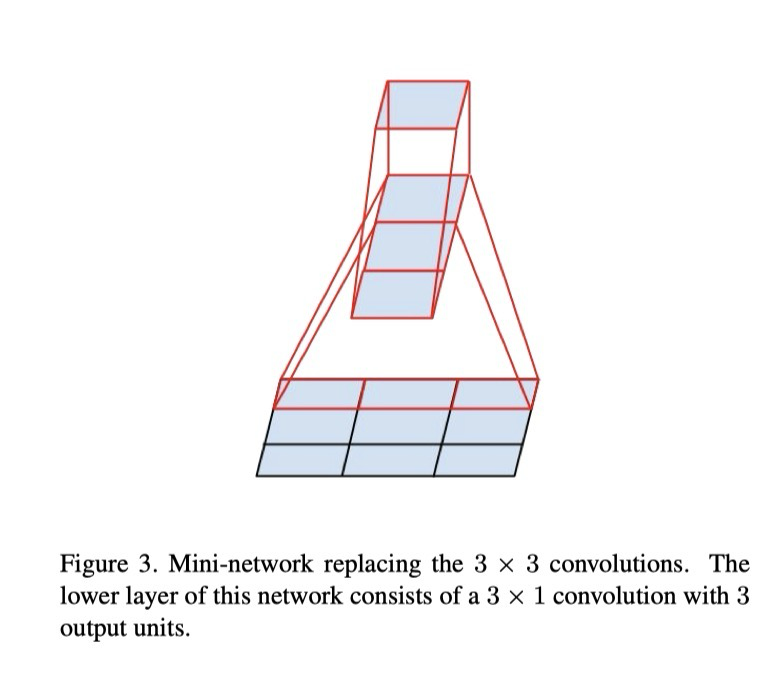
앞선 결과들은 3×3보다 큰 필터를 갖는 합성곱은 일반적으로 유용하지 않음을 시사한다. 왜냐하면 이들은 항상 일련의 3×3 합성곱 층으로 분해할 수 있기 때문이다. 그렇다면 이들을 더 작은 예, 2×2 합성곱으로 분해하는 것이 좋을까? 그러나 실제로는 비대칭 합성곱(asymmetric convolution)을 사용하면 2×2보다 더 나은 결과를 얻을 수 있다. 예를 들어, 3×1 합성곱에 이어 1×3 합성곱을 사용하는 것은 3×3 합성곱과 동일한 수용 영역(receptive field)을 갖는 2층 네트워크를 적용하는 것과 같다(그림 3 참조). 이 경우 입력과 출력 필터 수가 동일하다면, 두 층 해법은 동일한 출력 필터 수에 대해 연산량이 33% 더 저렴하다. 반면, 3×3 합성곱을 두 개의 2×2 합성곱으로 분해하면 연산 절감은 겨우 11%에 불과하다.
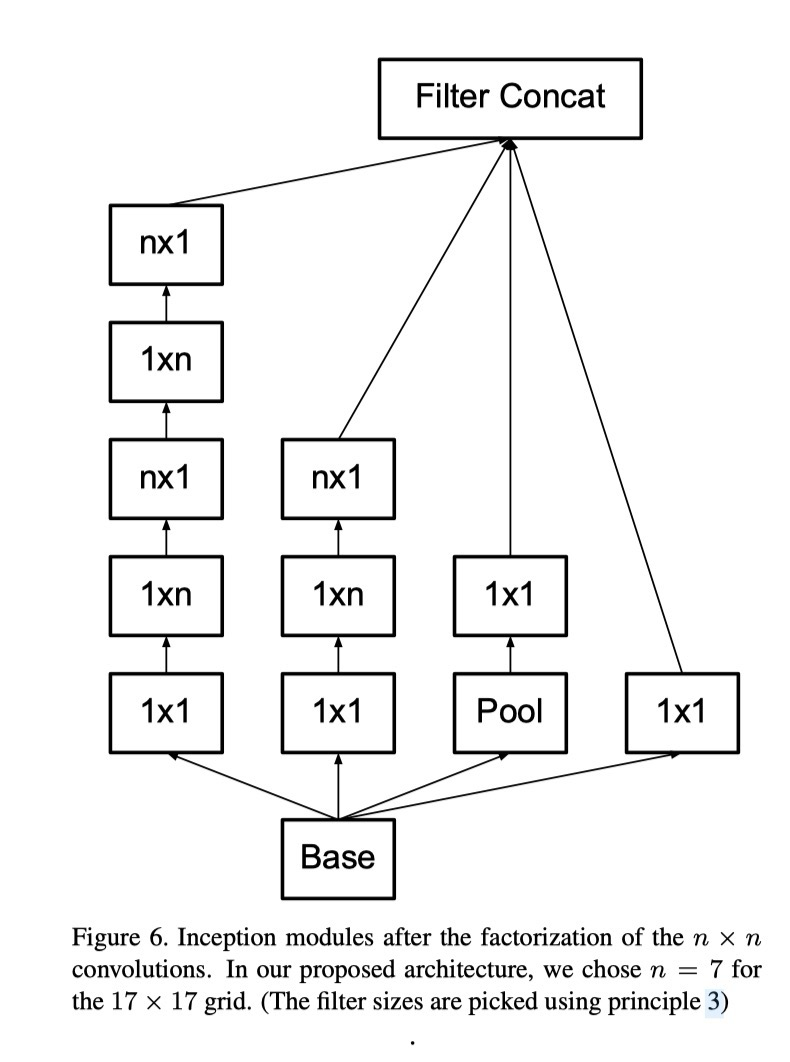
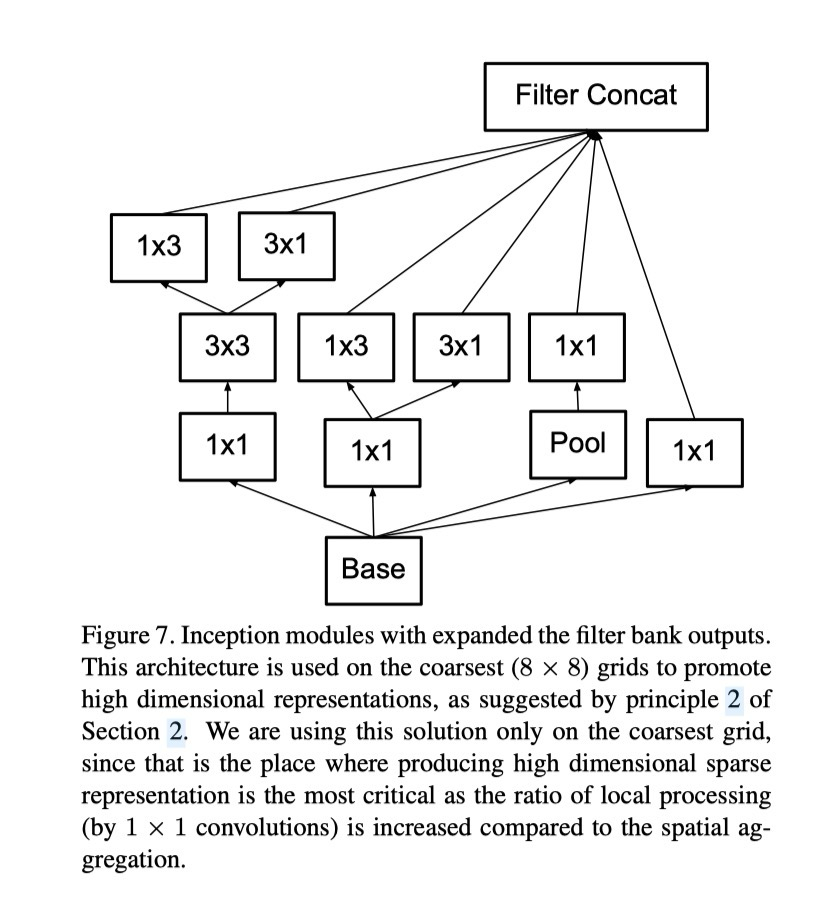
이론적으로는 더 나아가 모든 n×n 합성곱을 1×n 합성곱과 n×1 합성곱으로 대체할 수 있으며, n이 커질수록 계산 비용 절감 효과는 더욱 커진다(그림 6 참조). 실제로는 이러한 분해가 네트워크의 초기 층에서는 잘 작동하지 않았으나, 중간 크기 그리드(m×m feature map, m≈12~20)에서는 매우 좋은 결과를 보였다. 이 수준에서는 1×7 합성곱에 이어 7×1 합성곱을 사용하는 것이 효과적임을 확인하였다.
내용
- GoogleLeNet에서의 초기 성능 향상 대부분은 차원축소의 적극적인 활용에서 기인한다.
- 합성곱 분해(facotrizing convolutions)의 특수한 사례로 볼 수 있다.
- e.g. 큰 합성곱 대신, 1x1 -> 3x3 합성곱을 두는 경우 : 비전 네트워크에서 인접값들이 강한 상관으로 기대할 수 있고, 이는 곳 conv를 하기전에 차원을 줄여도 표현력있는 local 표현을 얻을 수 있다.
- 5×5 합성곱은 연산량이 3×3 합성곱의 약 2.78배. 하지만 2개의 3×3 합성곱으로 대체하면 연산량과 파라미터 수를 크게 줄일 수 있다.
- 합성곱 분해(facotrizing convolutions)의 특수한 사례로 볼 수 있다.
- 합성곱 분해의 계산 효율성을 높이는 것을 목표로 한다.
- 더 큰 합성곱은 연산 비용 면에서 불균형적으로 비싸다.
- 5x5하나보다 3x3두개가 비용면에서 2.78배 저렴하다.
- 단점 : 더 넓은 영역의 의존성을 포착 가능 -> 표현력이 높아진다.
- 단점 : 더 넓은 영역의 의존성을 포착 가능 -> 표현력이 높아진다.
- 5x5하나보다 3x3두개가 비용면에서 2.78배 저렴하다.
- 5x5 계산을 보면 작은 네트워크가 슬라이딩 하는것과 유사하게 움직인다.
- translation invariance를 활용하여, 작은 완전 연결층(3x3) 2개를 연결시키는것이 자연스럽다.
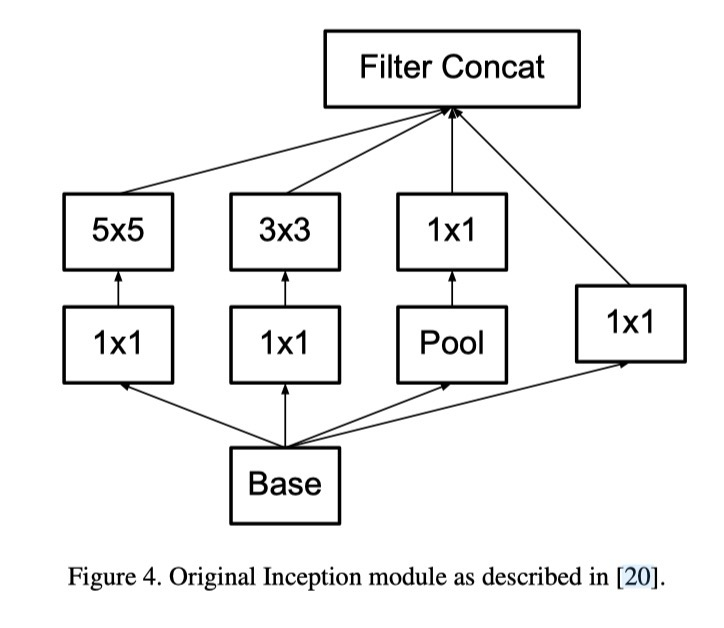
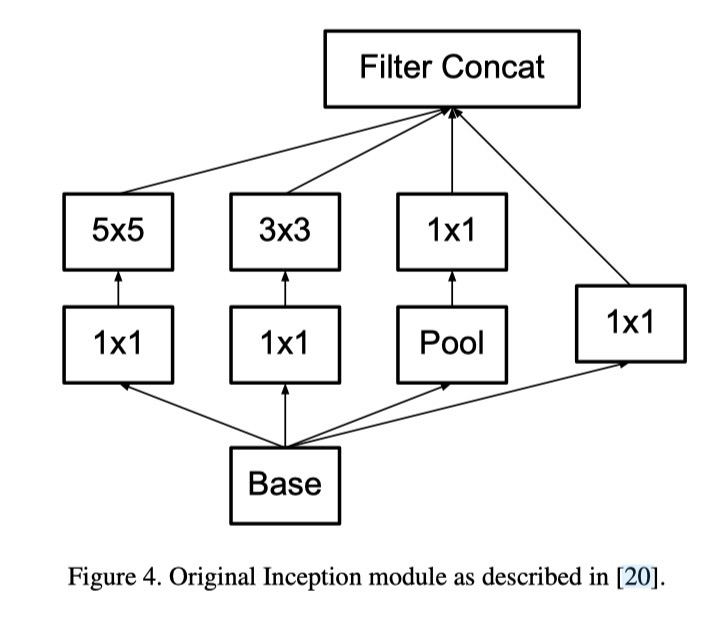
- 3x3두개로 분해시, 연산량이 28%줄어들게 된다
- $n=alpha*m$ 일때, 5x5를 3x3 2개로 바꾸게 되면, $\sqrt{\alpha}$ 만큼 필터를 늘리는게 합리적이다.
- 그러나 인접타일 즉 재사용이 가능하기 때문에, 연산량은 (9+9)/25 = 18/25로 줄어, 28%절감된다.
- 그러나 두가지 의문점이 든다
- 표현력 감소
- 선형 부분 분해가 목적이라면 첫번째 층을 선형함수를 유지하는것이 좋지 않는가?
- 그러나 실험결과 ReLU가 다른 Linear보다 효과적이다
- 성능이 향상되는 이유는 Linear보다 ReLU+배치정규화가 보다 넓은 표현력을 제공하기 때문이라고 판단된다. 즉 표현력 보장과 연산량 감소가 보장된다.
3.2. Spatial Factorization into Asymmetric Convolutions
- 대칭합성곱과 비대칭합성곱중 비대칭 합성곱이 더 나은 효과를 얻을 수 있다.
- 3x1 -> 1x3 네트워크
- 3x3을 2층구조로 적용한것과 같다
- 그러나 3x3을 2x2두개로 적용하는경우 효율성은 11%증가에비해 3x1, 1x3으로 적용시 33%저렴하다
- 이러한 nxn -> nx1 + 1xn분해는 초기층에서는 효과가 없었느나, 중간층(mxm, 12<= m <=20)에서는 유용하다. 또한 n이 커질수록 절감률이 상승한다.
포인트
| 목 | 내용 |
|---|---|
| 문제 | 큰 필터(5×5, 7×7)는 연산량/파라미터 수가 과도하게 큼 |
| 접근법 | 작은 필터(3×3, 1×1)로 분해하여 동일한 수용영역(receptive field) 확보 |
| 기대 효과 | 연산 효율 ↑, 파라미터 수 ↓, 학습 속도 ↑ |
| 응용 | Inception 모듈의 효율적 설계 핵심 원리 중 하나 |
핵심 메시지: 큰 합성곱을 작은 합성곱의 조합으로 대체하면 효율성과 표현력을 동시에 확보할 수 있다.
3.1. Factorization into smaller convolutions
| 항목 | 내용 |
|---|---|
| 문제 | 5×5 합성곱 → 3×3 합성곱보다 2.78배 비쌈 |
| 접근법 | 5×5 합성곱 ≈ 3×3 합성곱 2개로 분해 |
| 절감 효과 | 연산량 약 28% 절감, 파라미터 수 동일 비율 절감 |
| 활성화 선택 | ReLU가 linear보다 성능 우수 (BN과 결합 시 특히 효과적) |
| 의의 | 효율적 구조 설계 + 표현력 유지/강화 |
핵심 메시지: 큰 합성곱은 작은 합성곱의 조합으로 효율적으로 대체 가능하며, ReLU 활성화와 배치 정규화를 결합할 때 가장 효과적이다.
3.2. Spatial Factorization into Asymmetric Convolutions
| 항목 | 내용 |
|---|---|
| 문제 | 큰 합성곱(예: 3×3, 5×5)은 연산량이 과다 |
| 접근법 | 대칭 → 비대칭 분해 (예: 3×3 → 3×1 + 1×3) |
| 절감 효과 | 대칭 분해(2×2): 11% 절감 / 비대칭 분해(3×1+1×3): 33% 절감 |
| 일반화 | n×n 합성곱 → 1×n + n×1, n 증가 시 절감 효과 확대 |
| 한계 | 초기 층에서는 효과 없음, 중간 그리드(12≤m≤20)에서 효과적 |
핵심 메시지: 큰 합성곱은 비대칭 작은 합성곱으로 분해할 때 계산 효율이 가장 크며, 특히 중간 수준 feature map에서 성능과 효율성을 동시에 얻을 수 있다.
📚 4. Utility of Auxiliary Classifiers
번역
[20]에서는 매우 깊은 네트워크의 수렴(convergence)을 개선하기 위해 보조 분류기(auxiliary classifier) 개념을 도입하였다. 원래 동기는 유용한 그래디언트를 하위 계층으로 전달하여 즉시 활용할 수 있도록 하고, 매우 깊은 네트워크에서 발생하는 그래디언트 소실(vanishing gradient) 문제를 완화하여 학습 수렴을 개선하는 것이었다. 또한 Lee et al [11]은 보조 분류기가 학습을 더 안정적이고 수렴을 더 좋게 한다고 주장했다.
그러나 저자들의 실험에 따르면, 보조 분류기는 학습 초기 단계에서 수렴 개선에 기여하지 않았다. 보조 분류기가 있는 네트워크와 없는 네트워크는 둘 다 높은 정확도에 도달하기 전까지 학습 진행 양상이 거의 동일했다. 하지만 학습 후반부에 이르면, 보조 분류기를 가진 네트워크가 없는 네트워크의 정확도를 추월하여 약간 더 높은 성능에 도달했다.
또한 [20]에서는 네트워크의 서로 다른 단계에 두 개의 보조 분류기를 배치하였다. 그러나 더 하위 단계의 보조 분류기를 제거해도 최종 성능에는 부정적인 영향을 주지 않았다. 앞 단락의 관찰 결과와 결합하면, [20]에서 주장한 “이 보조 분류기가 저수준 특징(low-level features)의 학습을 돕는다”는 가설은 잘못되었을 가능성이 높다. 대신, 저자들은 보조 분류기가 정규화자(regularizer)로 작용한다고 주장한다. 이는 보조 분류기에 배치 정규화(batch normalization)나 드롭아웃(dropout)을 적용했을 때 주 분류기의 성능이 향상되는 사실로 뒷받침된다. 이는 또한 배치 정규화가 정규화자로 작용한다는 추측에 대한 약한 증거이기도 하다.
내용
- 보조 분류기(auxiliary classifier) : 유용한 gradient를 하위 계층에 전달하고, 깊은 네트워크에서 발생할 수 있는 기울기 소실 현상을 방지하여 학습 수련을 개선하고, 안정적이게 그리고 수렴을 좋게 한다고 이전 저자들을 주장했다.[GoogLeNet]
- 그러나, 초기층의 경우 보조 분류기는 학습 개선에 도움을 주지 않았으며, 후반부에 조금 효과가 있었다.
- 그리고, 두개 이상의 분류기를 배치했을때, 하위 분류기는 저수준 학습 특징을 돕는다는 효과보다는 정규화 효과가 있다고 판단되어 진다. 이는 후반부에 보조 분류기에 Dropout이나 BN을 적용하면 효과가 있다고 판단된다.
- 즉 저수준 학습 보조장치가 아니라, 정규화장치이다.
포인트
| 항목 | 내용 |
|---|---|
| 원래 가설 | 그래디언트 소실 방지, 저수준 특징 학습 촉진 |
| 관찰 결과 | 초기 수렴에는 영향 없음, 학습 후반에서 성능 소폭 향상 |
| 새로운 해석 | 보조 분류기 = 정규화자 (regularizer) |
| 근거 | BN/Dropout 적용 시 성능 ↑, 배치 정규화가 정규화자 역할을 한다는 증거 |
핵심 메시지: 보조 분류기는 단순히 그래디언트 소실 방지 장치가 아니라, 네트워크의 일반화 성능을 높이는 정규화 장치로 해석하는 것이 타당하다.
📚 5. Efficient Grid Size Reduction
번역
전통적으로 합성곱 신경망은 특성 맵(feature map)의 그리드 크기를 줄이기 위해 풀링(pooling) 연산을 사용했다. 표현 병목(representational bottleneck)을 피하기 위해, 최대 풀링이나 평균 풀링을 적용하기 전에 네트워크 필터의 활성화 차원을 확장하는 방식을 사용했다. 예를 들어, d×d 그리드에 k개의 필터가 있을 때 d/2 × d/2 크기의 그리드에 2k 필터를 얻고자 한다면, 먼저 stride-1 합성곱(2k 필터)을 수행한 뒤 추가 풀링 단계를 적용해야 한다. 이 경우 전체 연산 비용은 큰 그리드에서의 무거운 합성곱에 의해 지배되며, 연산량은 약 2d²k²에 이른다.
한 가지 대안은 합성곱과 풀링을 결합하여 stride-2 합성곱으로 바로 줄이는 것이다. 이 경우 연산량은 2(d/2)²k²로 줄어들어 계산 비용이 1/4로 감소한다. 그러나 이 방식은 표현 병목을 초래한다. 전체 표현 차원이 (d/2)²·2k로 줄어들어 네트워크 표현력이 감소하기 때문이다(그림 9).
이에 저자들은 계산 비용을 더 줄이면서도 표현 병목을 피하는 또 다른 방식을 제안한다(그림 10). 즉, 두 개의 병렬 stride-2 블록을 사용하는 것이다: P는 풀링 계층(최대 풀링 또는 평균 풀링), C는 stride-2 합성곱 계층이다. 이 두 출력을 필터 차원에서 연결(concatenate)하여 최종 출력을 얻는다.
내용
- 전통적인 CNN의 featuremap은 그리드 크기를 줄이기 위해 pooling연산을 사용했음.
- 병목 현상을 피하기 위해 max, mean을 적용하기 전에 네트워크의 필터차원을 확장하는 방식을 사용했다.
- e.g. dxd그리드에 k개의 필터가 있을때 d/2 x d/2 크기의 그리드의 2k필터를 얻길 원한다면 stride1에 추가 풀링을 수행해야 하며 연산량은 $2{d^2}{k^2}$에 이른다.
- 즉 conv -> pooling형식
- 풀링과 stride2를 결합하여 합성곱을 바로 줄여버리면 이 연산량은 $2{(d/2)}^2{k^2}$로 줄어들어 비용이 25%로 감소한다. 그러나 이 방식은 병목을 초래한다.
- 전체 표현 차원이 ${(d/2)^2}*2k$로 줄어듦
- 즉, conv(s=2)
- 이에 새로운방식을 제안
- 풀링과 conv를 동시에 수행해서, 필터차원에서 연결하여 최종 출력을 얻는다
일반 방법: d×d, k 필터 → (d/2)×(d/2), 2k 필터
- stride-1 conv (2k) + pooling → 연산량 크다 (2d²k²)
대안: stride-2 conv만 → 연산량 줄지만 병목 발생 (표현력 저하)
- 제안 방법: stride-2 풀링(P) + stride-2 conv(C)를 병렬로 수행 후, 필터 차원에서 concatenate
포인트
| 항목 | 내용 |
|---|---|
| 기존 방식 | stride-1 conv (2k 필터) + pooling → 연산량 과다 |
| 단순 대안 | stride-2 conv만 사용 → 연산량 감소, 하지만 표현력 저하 |
| 제안 방법 | stride-2 풀링과 stride-2 합성곱을 병렬 적용 후 concatenate |
| 효과 | 연산 효율성과 표현력(비병목) 동시 확보 |
핵심 메시지: 그리드 크기를 줄일 때 풀링과 합성곱을 병렬로 사용하면 연산 효율성과 표현력 보존을 동시에 달성할 수 있다.
📚 6. Inception-v2
번역
앞서 제시한 아이디어들을 종합하여, ILSVRC 2012 분류 벤치마크에서 성능을 개선한 새로운 아키텍처를 제안한다. 네트워크의 전체 구조는 표 1에 제시되어 있다. 먼저 전통적인 7×7 합성곱을 3개의 3×3 합성곱으로 분해하였다(3.1절에서 설명한 아이디어). Inception 부분에서는 35×35 해상도에서 각 288 필터를 갖는 전통적 Inception 모듈 3개를 사용한다. 이는 5장에서 설명한 그리드 축소(grid reduction) 기법을 통해 17×17 그리드, 768 필터로 축소된다. 그 뒤에는 그림 5와 같은 분해된 Inception 모듈 5개가 이어진다. 다시 그림 10의 그리드 축소 기법을 사용하여 8×8×1280 그리드로 축소된다. 가장 작은 8×8 수준에서는 그림 6과 같은 Inception 모듈 2개를 배치하며, 이때 각 타일의 출력 필터 뱅크는 2048로 연결(concatenate)된다.
Inception 모듈 내부 필터 뱅크 크기를 포함한 상세 구조는 부록 자료에 제공된다.
표 1. 제안된 네트워크 아키텍처 개요 (각 모듈의 출력은 다음 모듈의 입력이 됨).
| 연산 종류 (패치 크기/스트라이드 또는 설명) | 입력 크기 |
|---|---|
| conv 3×3/2 | 299×299×3 |
| conv 3×3/1 | 149×149×32 |
| conv padded 3×3/1 | 147×147×32 |
| pool 3×3/2 | 147×147×64 |
| conv 3×3/1 | 73×73×64 |
| conv 3×3/2 | 71×71×80 |
| conv 3×3/1 | 35×35×192 |
| 3×Inception (그림 5 참조) | 35×35×288 |
| 5×Inception (그림 6 참조) | 17×17×768 |
| 2×Inception (그림 7 참조) | 8×8×1280 |
| pool 8×8 | 8×8×2048 |
| linear logits | 1×1×2048 |
| softmax classifier | 1×1×1000 |
내용
- 7x7필터를 3x3 3개로 분해
- inception 1 : 35×35×288
- inception 2 : 17×17×768
- inception 3 : 8×8×1280
포인트
| 항목 | 내용 |
|---|---|
| 입력 크기 | 299×299 RGB 이미지 |
| 주요 개선 | 7×7 conv 분해, Grid Reduction, Factorized Inception 모듈 |
| 특징 | 병목 방지, 효율적 연산, 높은 표현력 |
| 최종 출력 | 1000 클래스 분류 (ImageNet) |
핵심 메시지: Inception-v2는 큰 합성곱 분해, 효율적 그리드 축소, 비대칭 합성곱을 결합하여 적은 연산량으로 더 높은 표현력을 제공하는 아키텍처이다.
📚 7. Model Regularization via Label Smoothing
번역
여기서는 학습 중 라벨 드롭아웃의 주변화 효과를 추정하여 분류기 계층을 정규화하는 메커니즘을 제안한다.
각 훈련 예제 x에 대해 모델은 각 레이블 k ∈ {1 … K}의 확률을 계산한다:
| $p(k | x) = exp(z_k) / Σ_i exp(z_i)$ |
| 여기서 $z_i$는 로짓이다. 정답 분포 $q(k | x)$를 고려할 때, 손실은 다음과 같은 크로스 엔트로피이다: |
$ℓ = −Σ_k q(k) log p(k)$
단일 정답 라벨 y의 경우, $q(y) = 1$이고 $q(k) = 0 (k ≠ y)$이다. 따라서 크로스 엔트로피 최소화는 곧 정답 라벨의 로그우도 최대화와 같다. 그러나 이는 두 가지 문제를 초래한다:
과적합(overfitting): 모델이 지나치게 확신하게 된다.
적응성 감소: 가장 큰 logit이 다른 값보다 지나치게 커지면서 그래디언트가 포화되어 학습이 둔화된다.
| 저자들은 모델이 덜 확신하도록 유도하기 위해 다음 방법을 제안한다. 정답 라벨 y에 대해, 기존 $q(k | x) = δ_k,y$를 다음으로 치환한다: |
| $q′(k | x) = (1−ε)δ_k,y + εu(k)$ |
여기서 u(k)는 사전 분포(prior distribution)이며, 균등 분포(1/K)를 사용한다. 이를 라벨 스무딩 정규화(Label Smoothing Regularization, LSR)라 한다.
효과: 가장 큰 logit이 과도하게 지배적이 되는 것을 방지한다. 이는 크로스 엔트로피에 균등 분포와의 혼합을 추가한 것과 동일하다:
$H(q′, p) = (1−ε)H(q, p) + εH(u, p)$
ImageNet(K=1000)에서 $ε=0.1$을 적용했을 때, Top-1 및 Top-5 오류율이 약 0.2% 절대치로 감소하는 일관된 개선을 얻었다.
내용
- one-hot 인코딩은, 모델을 과도하게 확신하게 만들어 적응성 저하를 발생
- u(k)는 사전 분포(prior distribution)이며, 균등 분포(1/K)를 사용한 라벨 스무딩 정규화(Label Smoothing Regularization, LSR)을 사용
- logit이 지나치게 커지는것을 방지
- 일반화
- 실험적을 성능 향상
- 즉 정답라벨을 “살짝 흐리게”만들어 과적합을 막고 정규화 성능을 얻는다
- “이건 90% 확률로 개가 맞아. 하지만 나머지 10%는 다른 것일 수도 있다는 가능성을 열어두자”라고 가르치고, 10%의 확률을 다른 모든 라벨(고양이, 토끼 등)에 조금씩 나눠준다.
포인트
| 항목 | 내용 |
|---|---|
| 문제 | one-hot 라벨 → 과적합, logit 과도 지배, 학습 둔화 |
| 접근법 | 라벨 분포를 (1−ε)δ + ε·uniform 으로 스무딩 |
| 효과 | logit 균형 유지, 모델 일반화 ↑ |
| 실험 결과 | ImageNet, ε=0.1 → Top-1/Top-5 오류율 약 0.2% 절감 |
핵심 메시지: Label Smoothing은 단순하지만 강력한 정규화 기법으로, 모델이 덜 확신하게 만들어 과적합을 방지하고 일반화를 향상시킨다.
📚 8. Training Methodology
번역
본 연구에서는 TensorFlow [1] 분산 머신러닝 시스템을 사용하여 확률적 경사하강법(Stochastic Gradient)으로 네트워크를 학습하였다. 50개의 복제본(replica)을 구동했으며, 각 복제본은 NVidia Kepler GPU에서 batch size 32로 100 epoch 동안 학습되었다. 초기 실험에서는 momentum [19]을 사용하였으며 감쇠(decay)는 0.9였다. 그러나 최적 성능 모델은 RMSProp [21]을 사용했을 때 달성되었으며, decay=0.9, ε=1.0을 적용하였다.
학습률(learning rate)은 0.045로 설정하였고, 2 epoch마다 0.94의 지수 감쇠(exponential decay)를 적용하였다. 또한, 임계값 2.0의 gradient clipping [14]이 학습 안정화에 유용함을 확인하였다. 모델 평가 시에는 시간에 따라 계산된 파라미터의 이동 평균(running average)을 사용하였다.
내용
- 프레임워크: TensorFlow 분산 학습, GPU 50개 병렬 학습.
- 배치/에폭: batch size=32, 100 epochs.
- Optimizer 비교:
- Momentum (decay=0.9) → 초기 실험
- RMSProp (decay=0.9, ε=1.0) → 최적 결과
- 학습률 스케줄링: 초기값 0.045, 2 epoch마다 0.94배 감소 (exponential decay).
- Gradient Clipping: threshold=2.0 → 학습 안정화.
- 평가 방식: 파라미터의 이동 평균(running average)을 이용.
포인트
| 항목 | 내용 |
|---|---|
| 프레임워크 | TensorFlow 분산 학습 |
| 자원 | 50 GPU (Nvidia Kepler), replica 기반 |
| 배치/에폭 | batch size 32, 100 epochs |
| Optimizer | Momentum(초기) vs RMSProp(최적) |
| 학습률 | 0.045 시작, 2 epoch마다 0.94 배 감소 |
| 안정화 기법 | Gradient clipping (threshold 2.0) |
| 평가 | 파라미터 이동 평균(running average) |
핵심 메시지: Inception-v2/v3 학습에는 RMSProp, learning rate decay, gradient clipping, moving average 등 안정화 기법이 모두 결합되어 있으며, 이는 대규모 분산 학습 환경에서 안정적이고 효율적인 훈련을 가능하게 한다.
📚 9. Performance on Lower Resolution Input
번역
비전 네트워크의 전형적인 사용 사례 중 하나는 탐지 후 분류(post-classification of detection)이다. 예를 들어 Multibox [4]와 같은 경우로, 이는 이미지에서 단일 객체와 일부 문맥을 포함하는 작은 패치를 분석하는 것이다. 이때 과제는 패치의 중앙 부분이 어떤 객체에 해당하는지 여부를 판별하고, 객체가 있다면 그 클래스를 결정하는 것이다. 문제는 객체가 상대적으로 작고 저해상도라는 점이다.
일반적인 통념은 수용 영역(receptive field)이 클수록 인식 성능이 좋다는 것이다. 그러나 입력 해상도를 키우면 연산량도 증가한다. 반대로 단순히 해상도를 줄이면 연산량은 줄어들지만 성능이 크게 떨어진다. 공정한 비교를 위해서는 계산 비용을 일정하게 유지해야 한다.
저자들은 연산량이 거의 동일한 세 가지 실험을 수행했다:
299×299 수용 영역, stride=2, max pooling (기준).
151×151 수용 영역, stride=1, max pooling.
79×79 수용 영역, stride=1, pooling 없음.
| 수용 영역 크기 | Top-1 정확도 |
|---|---|
| 79×79 | 75.2% |
| 151×151 | 76.4% |
| 299×299 | 76.6% |
즉, 저해상도 네트워크는 학습 속도는 더 느리지만 최종 성능은 고해상도 네트워크와 큰 차이가 없었다. 그러나 단순히 해상도를 줄이고 모델 크기도 줄이면 성능이 크게 나빠진다. 따라서 표 2의 결과는 R-CNN 맥락에서 작은 객체를 다루기 위해 전용 고비용 저해상도 네트워크를 고려할 수 있음을 시사한다.
내용
| 항목 | 내용 |
|---|---|
| 연구 맥락 | 탐지 후 분류(post-classification), Multibox, 작은 객체 문제 |
| 가설 | 해상도 감소 → 성능 저하 |
| 접근법 | stride/pooling 조절하여 연산량 동일하게 맞춘 세 가지 설정 |
| 결과 | 성능 차이 미미 (최대 1.4%p), 단순 축소 모델은 성능 급락 |
| 시사점 | 작은 객체 탐지에서 저해상도 전용 네트워크 활용 가능 |
핵심 메시지: 입력 해상도가 낮아도 연산량을 보정하면 성능 손실은 크지 않으며, 이는 작은 객체 탐지에 특화된 네트워크 설계 가능성을 보여준다.
📚 10. Experimental Results and Comparisons
내용
- v2에 최적화를 진행한게 v3임