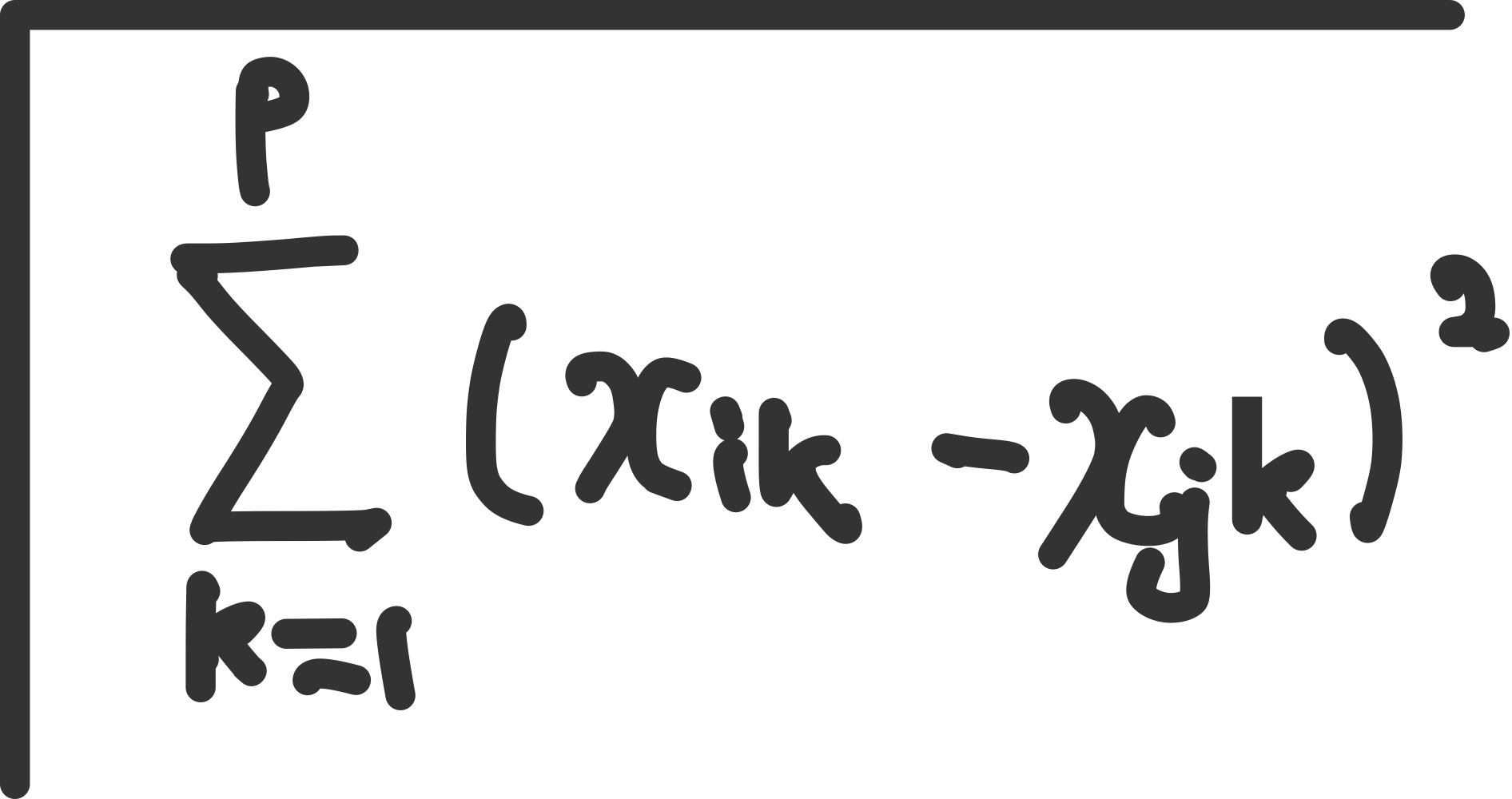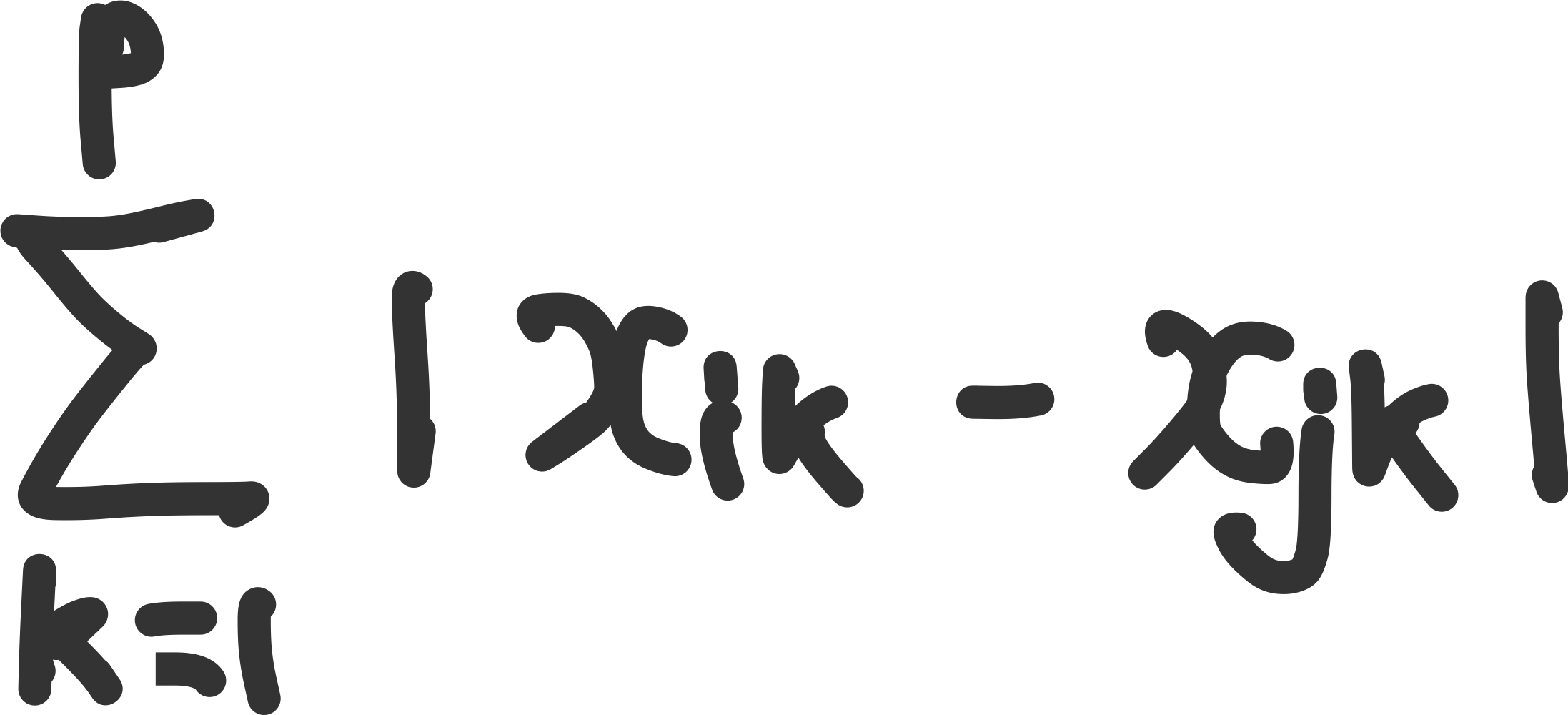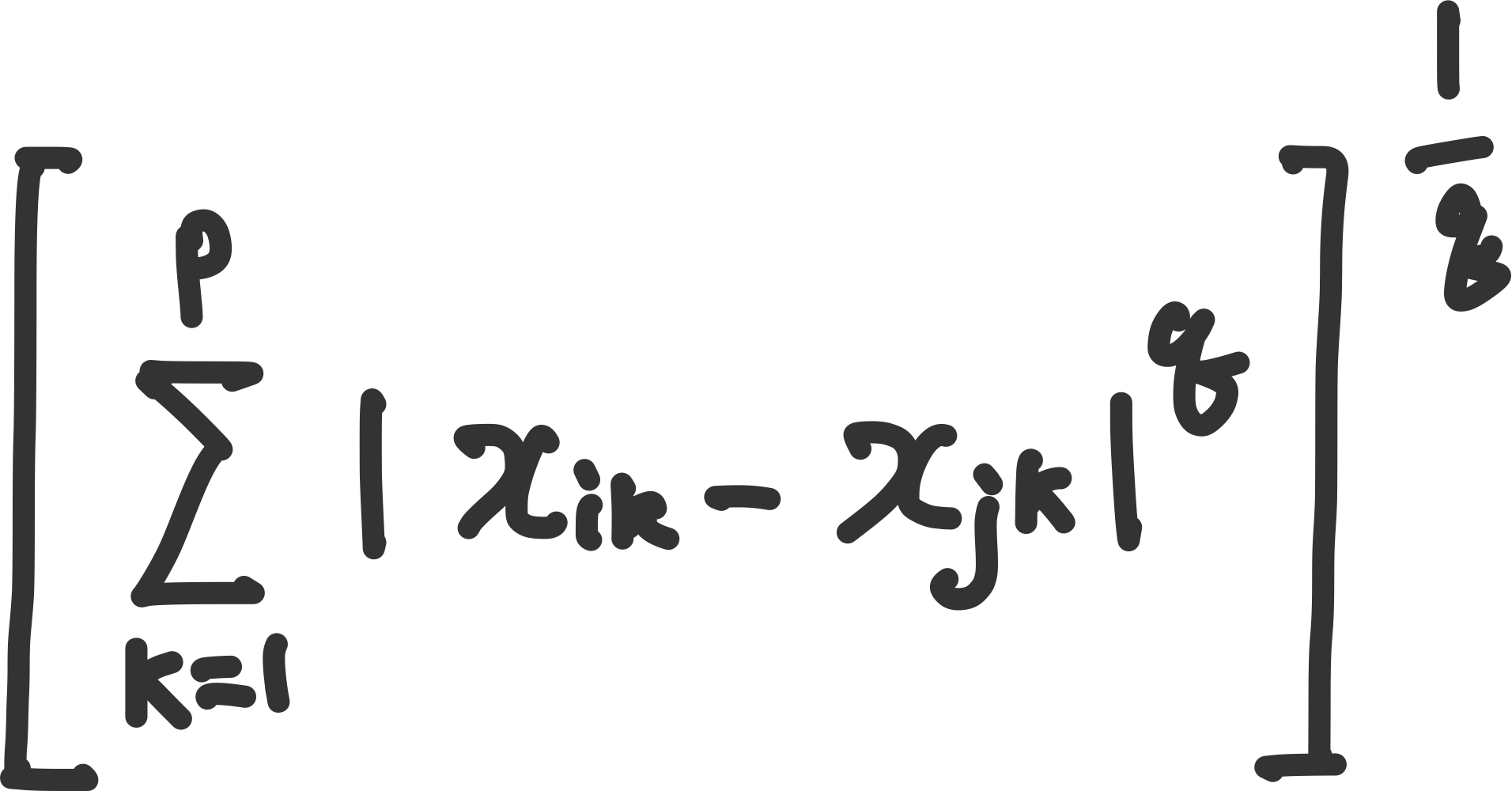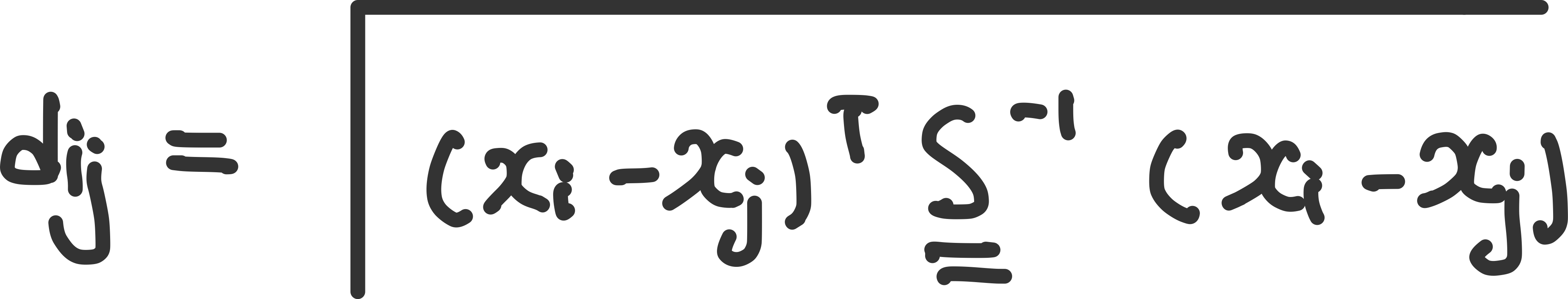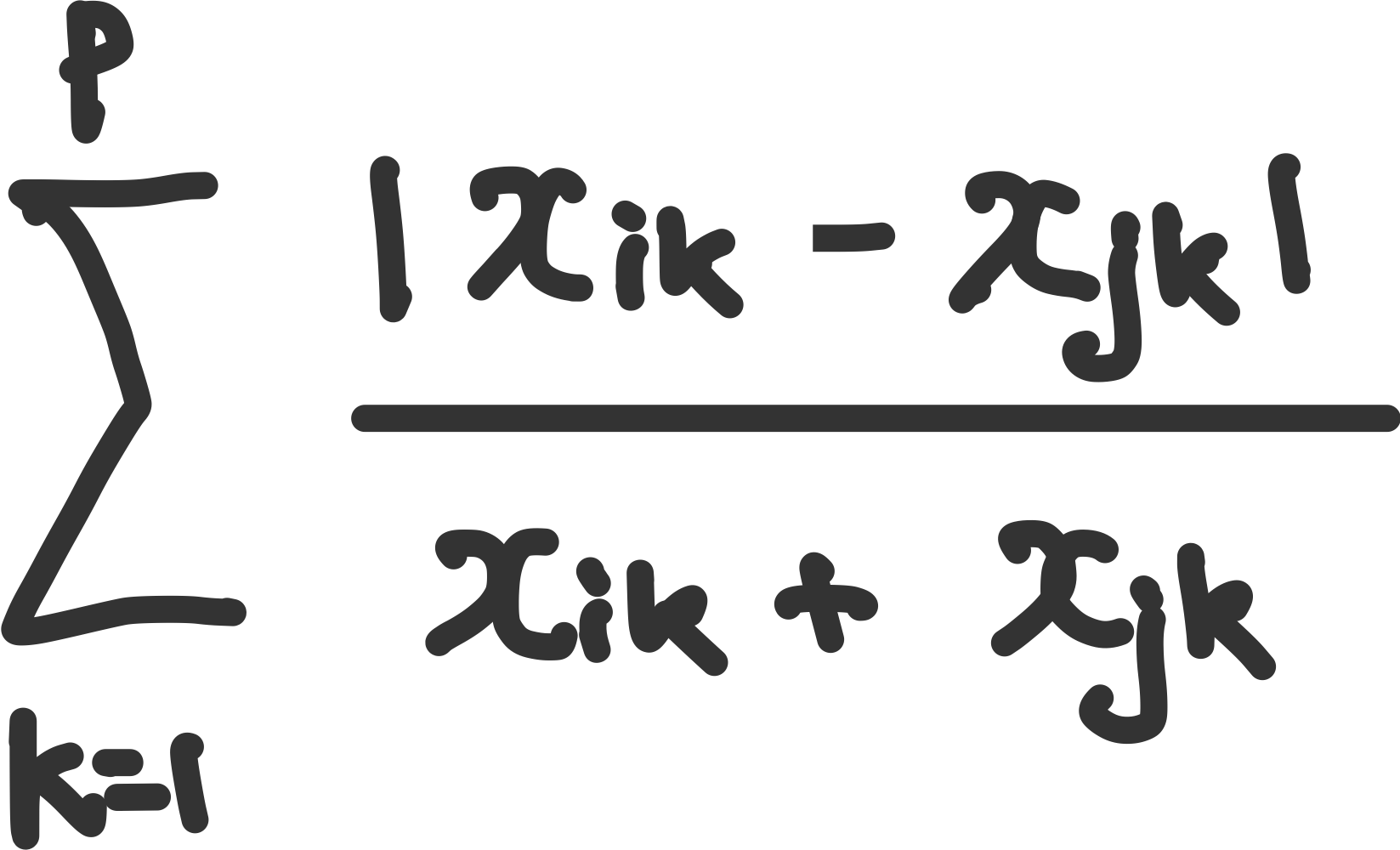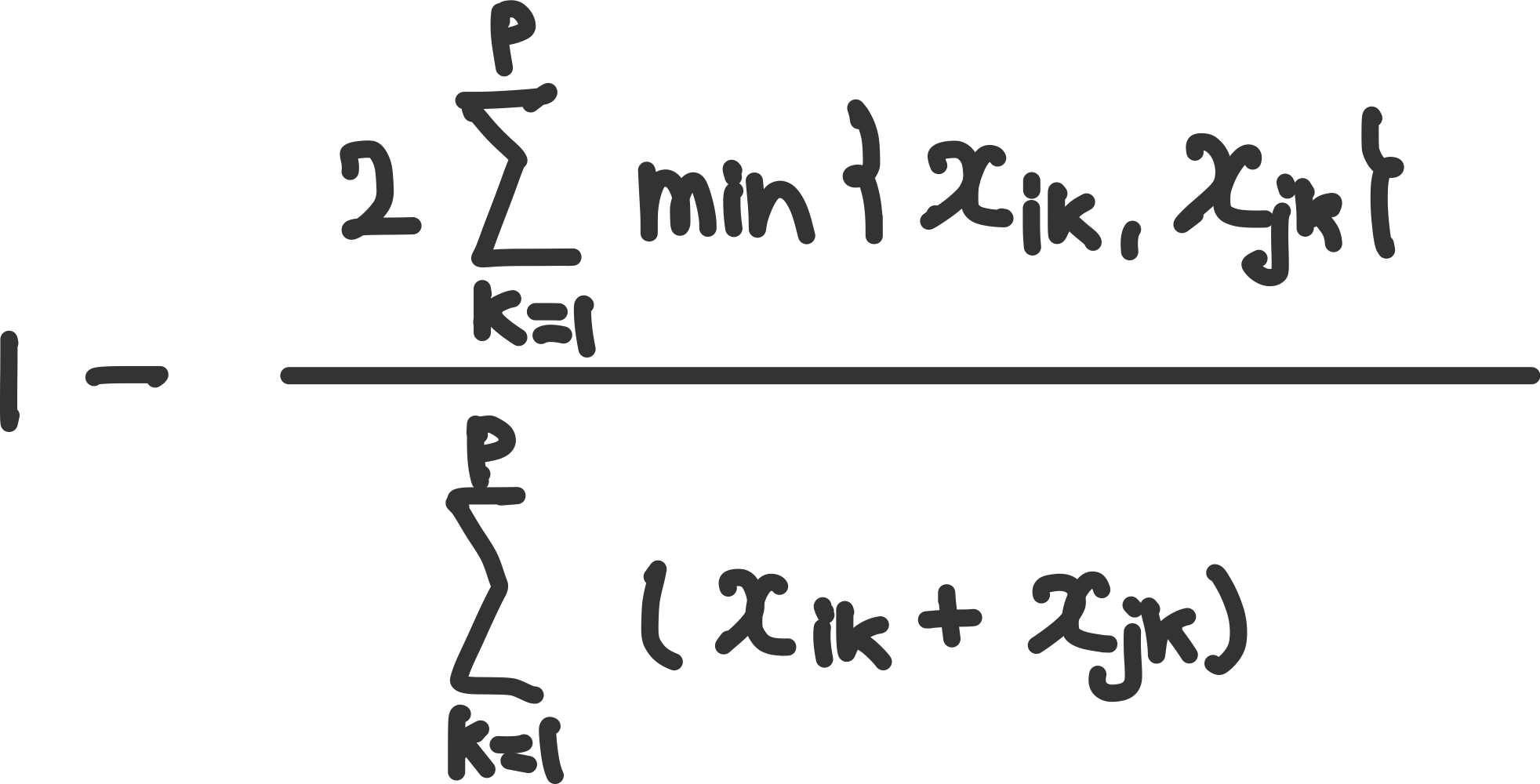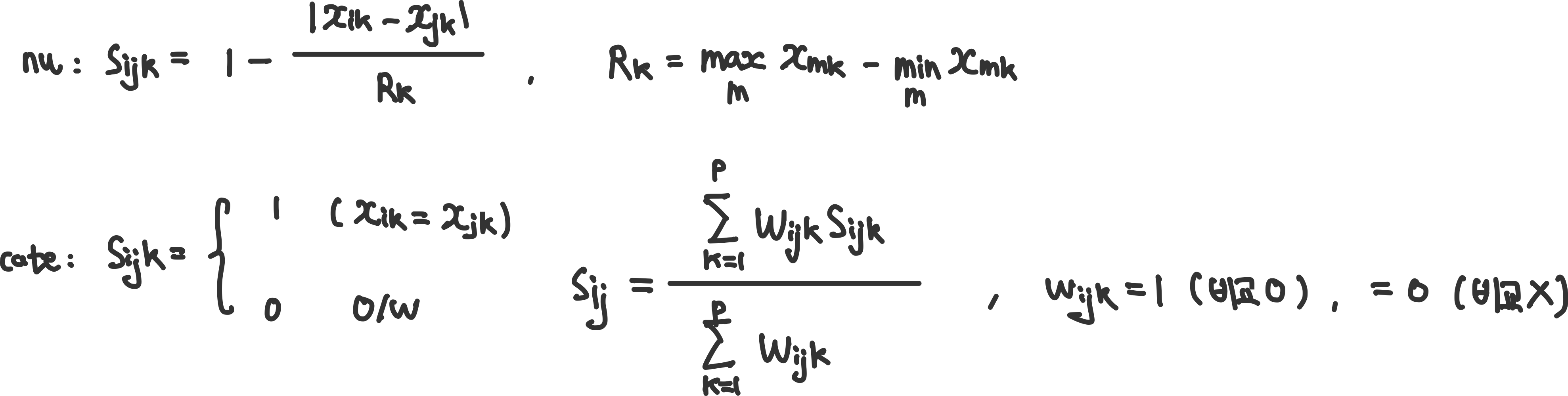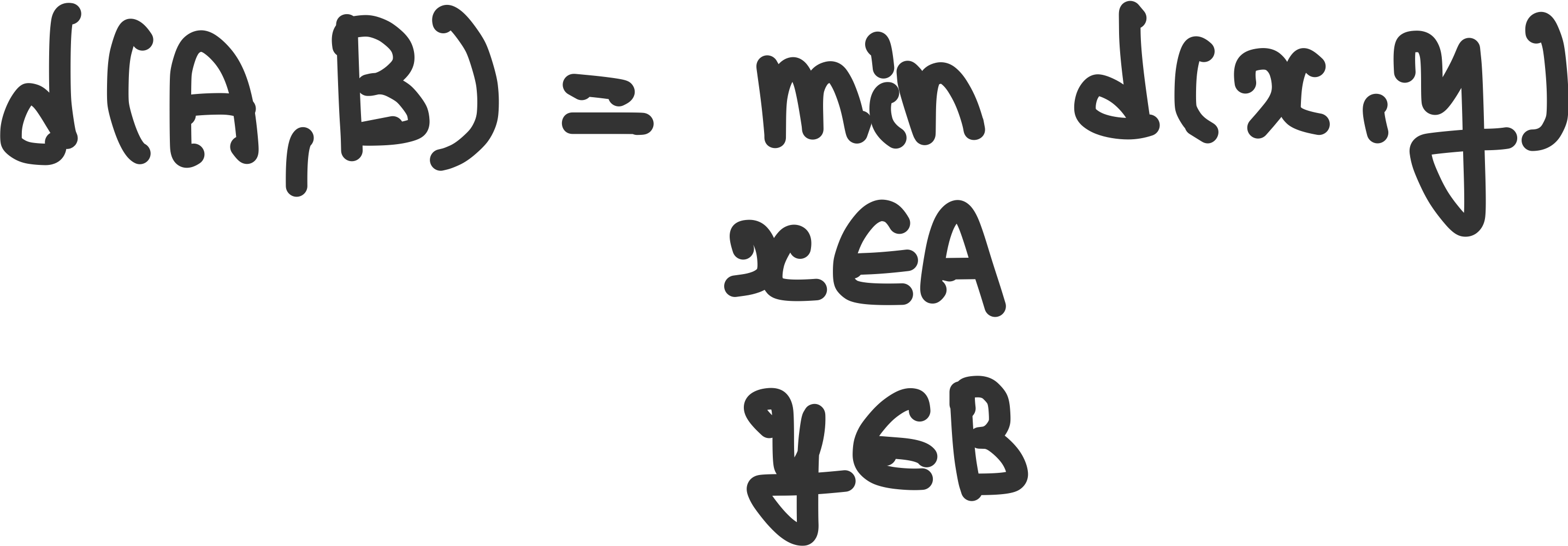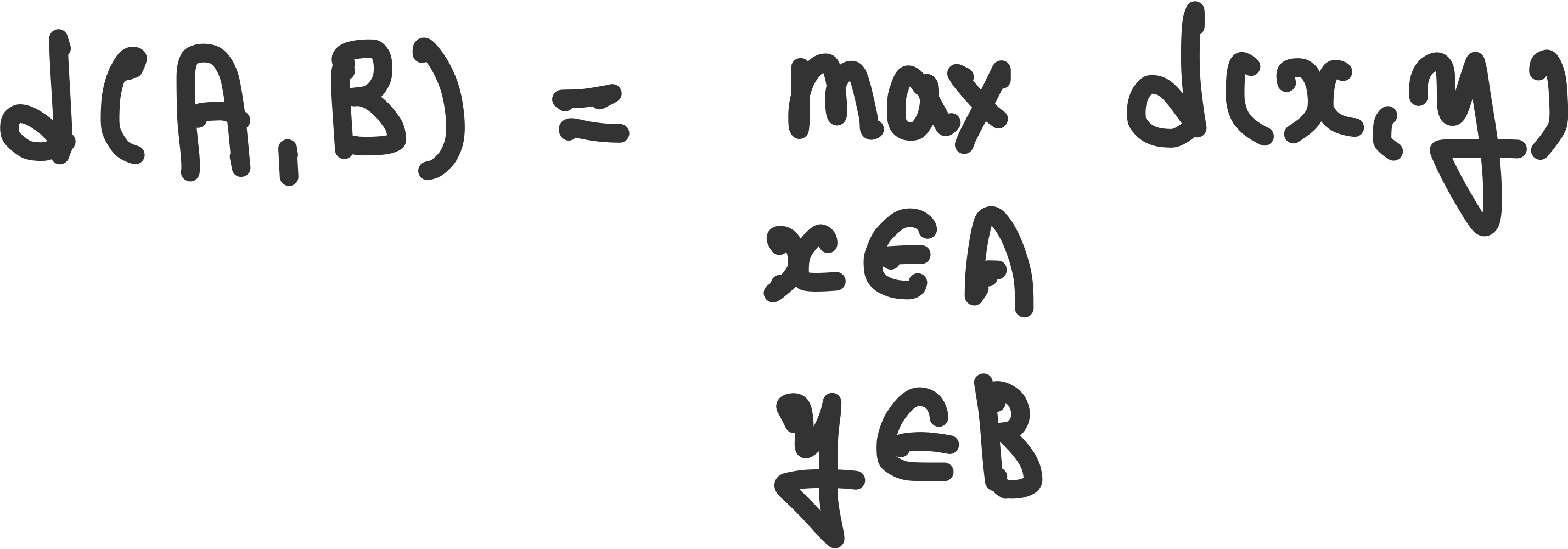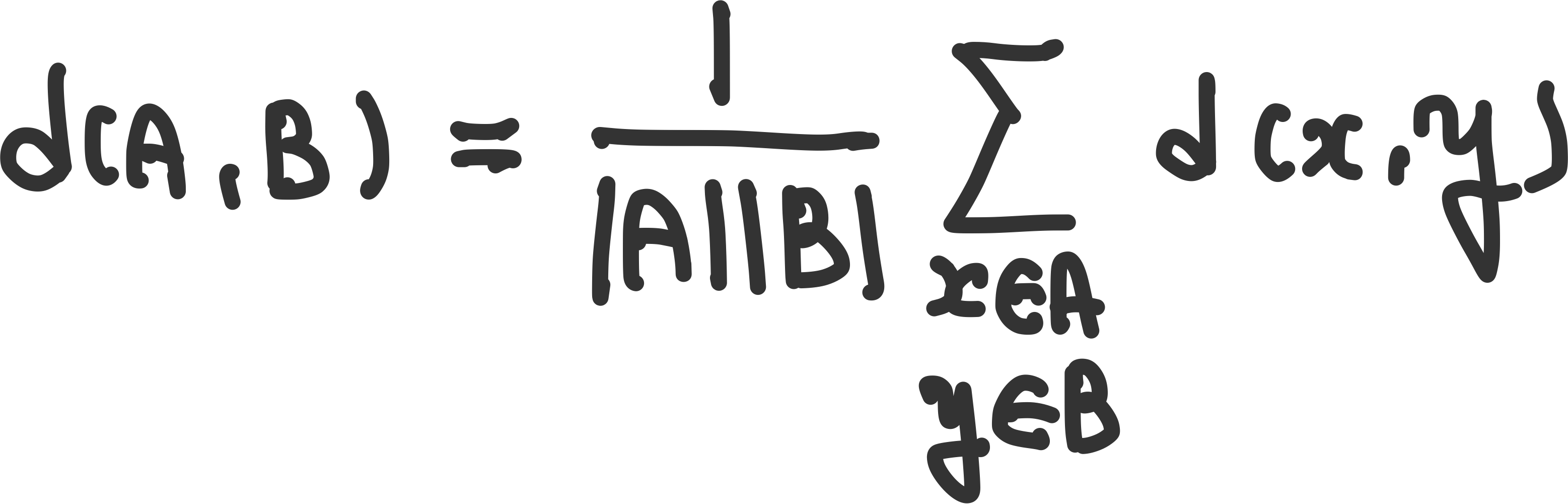Clustering(cont.)
Introduction
데이터를 “비슷한 것끼리” 묶는 비지도 학습(unsupervised learning)
- 목적
- 데이터의 집단[cluster, 어려운 말로 차원성(dimensionality)] 파악
- 이상치(outlier) 탐지
- 패턴파악
분류(classification) vs 클러스터링(clutering)
supervised(정답 있음, 그룹(레이블, 정답)이 미리 주어짐) vs unsupervised(그룹을 찾아냄, 비슷한것끼리 묶어줌)
종류
- 계층적(Hierarchical)
- 분할적(Partioning)
- Mixture Models
Similarity & Dissimilarity
유사도란 “비슷한 것 끼리 묶자”를 수치로 표현하는 방법
- row(행)을 묶을 때 : 거리(distance)
- col(열)을 묶을 때 : 상관계수(correlation)와 같은 연관도(association measure) 사용
대표적인 거리
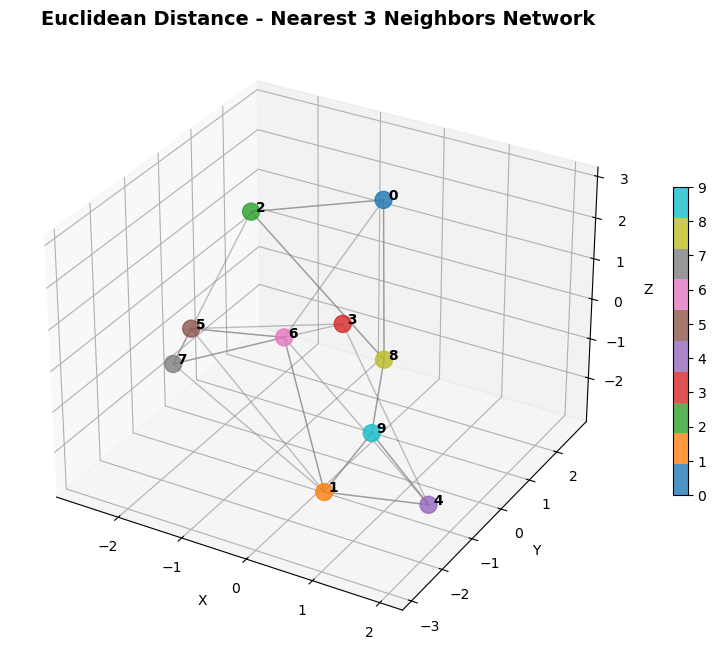
유클리드(euclidean, L2 norm)
피타고라스 거리 두 점을 잇는 가장 짧은 거리
범위 : $[0,∞)$, 0에가까울 수록 유사함
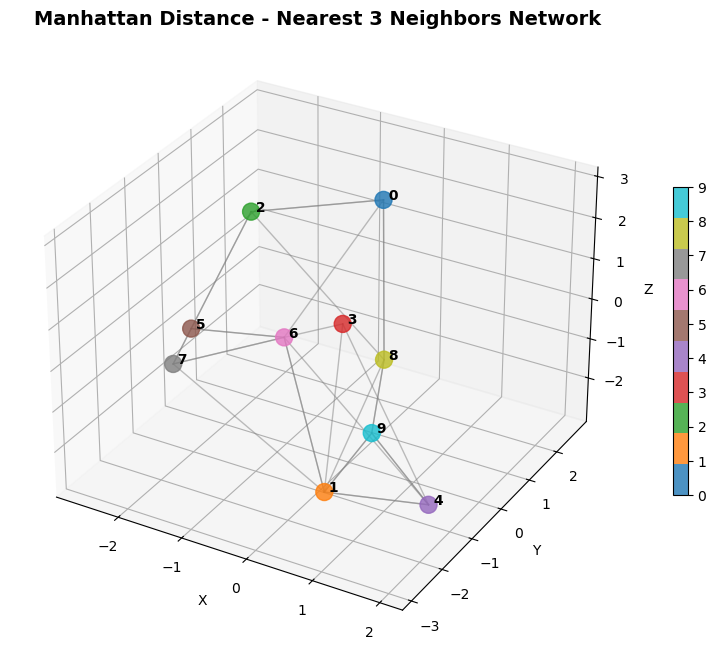
맨해튼 거리(manhattan, L1 norm)
택시 거리 격자를 따라 이동하는 가장 짧은 거리
[!NOTE]
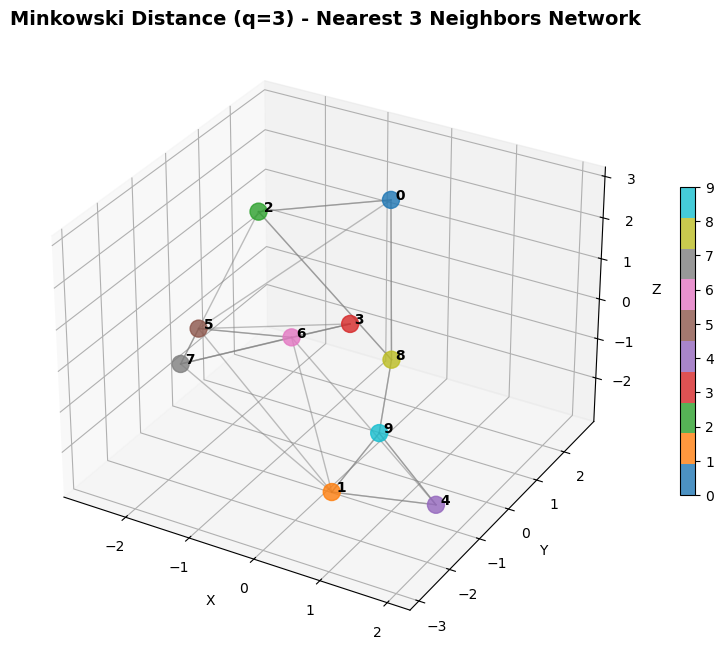
민코프스키 거리
q=1 : 맨해튼 거리
q=2 : 유클리드 거리
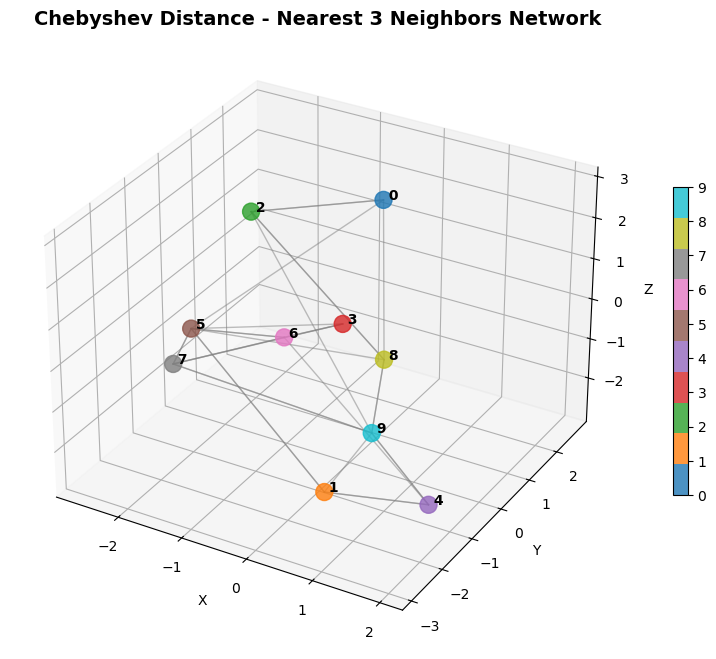
q 값이 커질 수록, 큰 차이의 좌표에 압도된다. 즉 가장 큰 좌표의 차이가 모든것을 압도하여 그 값만 남게된다. 즉 체스판에서 킹의 최소 움직임횟수와 동일하다. 따라서 체스판거리라고도 불리운다.
범위 : $[0,∞)$, 0에가까울 수록 유사함
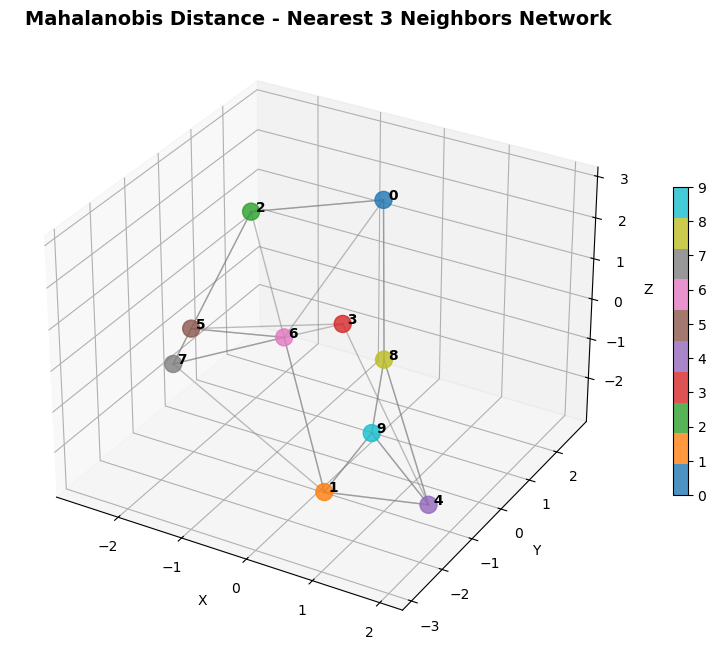
마할라노비스 거리(mahalanobis)
공분산을 고려하여 변수 스케일, 상관성까지 반영한 거리로 다차원 데이터에서 실제 분포 모양까지 고려
**범위 : $[0,∞)$, 0에가까울 수록 통계적으로 유사함
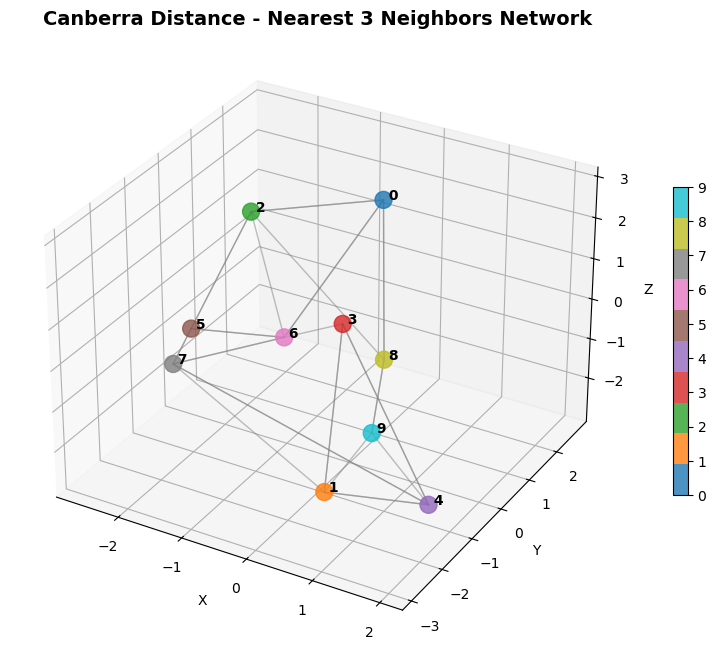
캔버라(canberra)
값이 0 근처일때 민감하게 반응하는 거리이며, 양의 값에서 주로 사용한다. 즉 작은값에 민감하게 반응하는 거리이다.
**범위 : $[0,∞)$, 0에가까울 수록 유사함
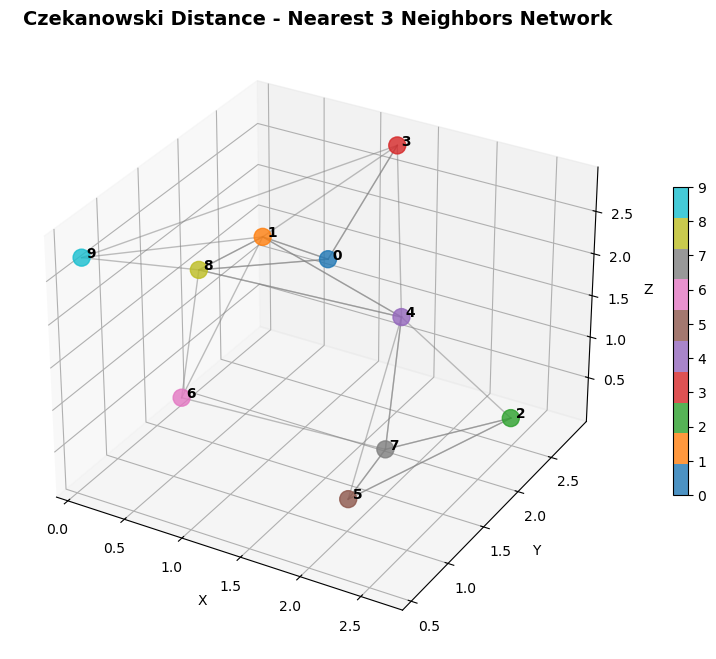
체카노프스키(Czekanowski)
두 대상이 얼마나 겹치는지에 대한 척도
**범위 : $[0,1]$, 1에가까울 수록 유사함
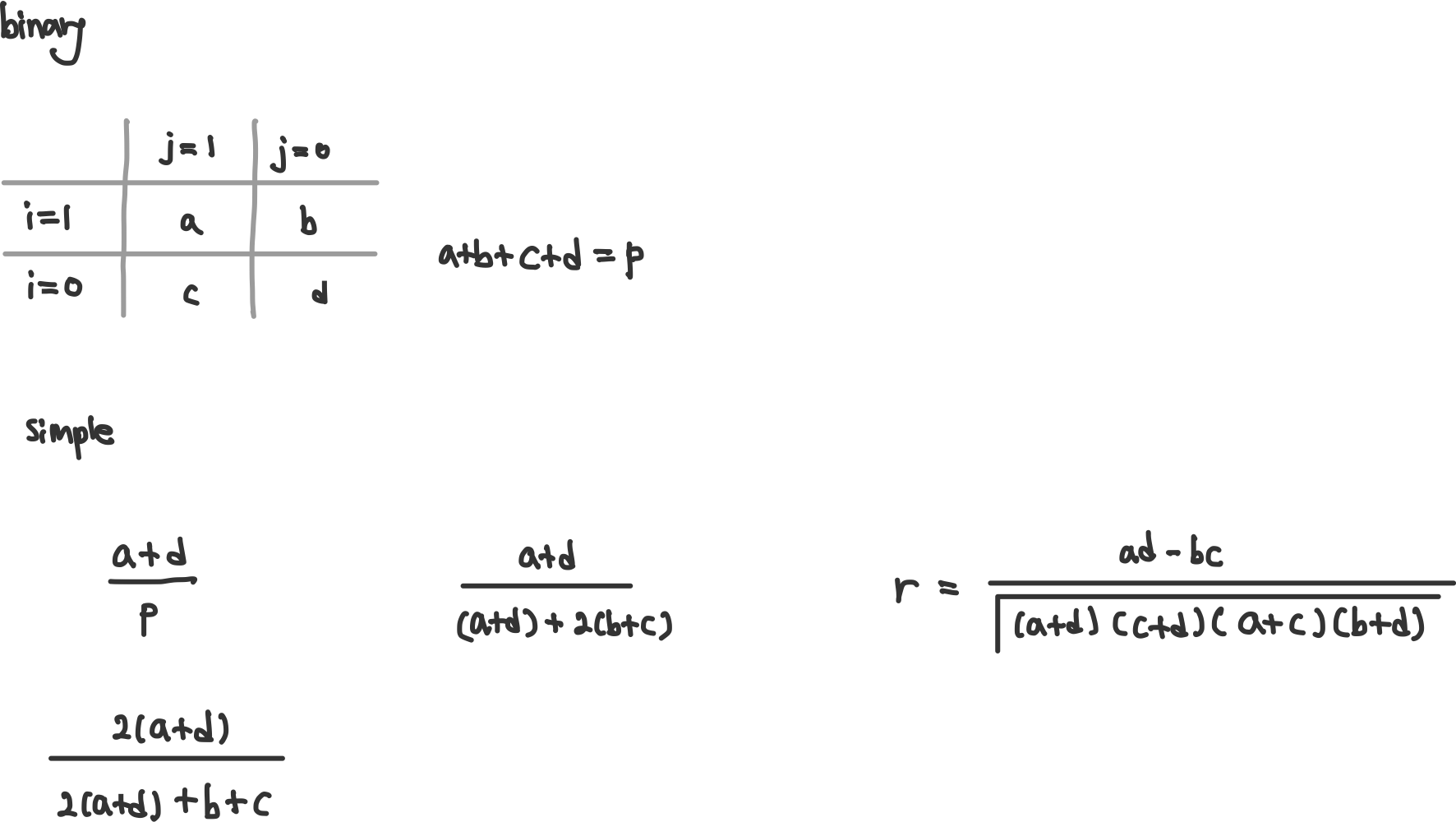
이진 변수 유사도
- 0-0을 유사하게 볼지, 유사하지않게 볼지에 따라 가중을 다르게 줄 수 있다. 즉 아니다-아니다가 같지 않을수도 같을수도 있다.
- e.g. 1 : 콜라를 사다, 0 = 콜라를 사지 않다. 0-0은 콜라를 사지 않는 경우에는 다른것을 사서 안 산 것일 수도 있다. 사이다-닥터페퍼 이런형식이다.
**범위 : $[0,1]$, 1에가까울 수록 유사함
Gower
혼합변수에 사용한다. 변수마다 $s_{ijk}$를 구한 후 한번에 계산한다.
**범위 : $[0,1]$, 1에가까울 수록 유사함
Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# L2 norm
import numpy as np
from scipy.spatial import distance
def pairwise_l2(P):
P = np.atleast_2d(P)
diff = P[:, None, :] - P[None, :, :] # (n,n,3)
return np.sqrt(np.sum(diff**2, axis=2)) # (n,n)
D_l2 = pairwise_l2(points)
# 검증
D_l2_sp = distance.squareform(distance.pdist(points, metric='euclidean'))
print("euclidean allclose:", np.allclose(D_l2, D_l2_sp))
D_l2[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# L1 norm
import numpy as np
from scipy.spatial import distance
def pairwise_l1(P):
P = np.atleast_2d(P)
diff = np.abs(P[:, None, :] - P[None, :, :])
return np.sum(diff, axis=2)
D_l1 = pairwise_l1(points)
# 검증
D_l1_sp = distance.squareform(distance.pdist(points, metric='cityblock'))
print("manhattan allclose:", np.allclose(D_l1, D_l1_sp))
D_l1[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# minkowski : q=3
import numpy as np
from scipy.spatial import distance
def pairwise_minkowski(P, q=3):
P = np.atleast_2d(P)
diff_q = np.abs(P[:, None, :] - P[None, :, :]) ** q
return np.sum(diff_q, axis=2) ** (1.0 / q)
q = 3
D_mink = pairwise_minkowski(points, q=q)
# 검증
D_mink_sp = distance.squareform(distance.pdist(points, metric='minkowski', p=q))
print(f"minkowski(q={q}) allclose:", np.allclose(D_mink, D_mink_sp))
D_mink[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# chebyshev
import numpy as np
from scipy.spatial import distance
def pairwise_chebyshev(P):
P = np.atleast_2d(P)
diff = np.abs(P[:, None, :] - P[None, :, :])
return np.max(diff, axis=2)
D_ch = pairwise_chebyshev(points)
# 검증
D_ch_sp = distance.squareform(distance.pdist(points, metric='chebyshev'))
print("chebyshev allclose:", np.allclose(D_ch, D_ch_sp))
D_ch[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# canberra
import numpy as np
from scipy.spatial import distance
def pairwise_canberra(P):
P = np.atleast_2d(P)
X = P[:, None, :] # (n,1,3)
Y = P[None, :, :] # (1,n,3)
num = np.abs(X - Y)
den = np.abs(X) + np.abs(Y)
frac = np.divide(num, den, out=np.zeros_like(num), where=(den != 0))
return np.sum(frac, axis=2)
D_can = pairwise_canberra(points)
# 검증
D_can_sp = distance.squareform(distance.pdist(points, metric='canberra'))
print("canberra allclose:", np.allclose(D_can, D_can_sp))
D_can[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# mahalanobis
import numpy as np
from scipy.spatial import distance
def pairwise_mahalanobis(P, S_inv):
P = np.atleast_2d(P)
X = P[:, None, :] # (n,1,3)
Y = P[None, :, :] # (1,n,3)
Δ = Y - X # (n,n,3)
d2 = np.einsum('ijk,kl,ijl->ij', Δ, S_inv, Δ) # 각 쌍의 제곱거리
return np.sqrt(np.maximum(d2, 0.0))
# 공분산 및 역행렬
S = np.cov(points.T, bias=False)
S_inv = np.linalg.pinv(S) # 정칙화/안정성 목적
D_mah = pairwise_mahalanobis(points, S_inv)
# 검증
D_mah_sp = distance.squareform(distance.pdist(points, metric='mahalanobis', VI=S_inv))
print("mahalanobis allclose:", np.allclose(D_mah, D_mah_sp))
D_mah[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# binary
import numpy as np
from scipy.spatial import distance
# 예시 이진 데이터 (3D 대신 0/1 피처로 시범)
np.random.seed(0)
bin_points = np.random.randint(0, 2, size=(10, 8)) # 10개 샘플, 8개 이진 피처
def pairwise_smc_distance(B):
B = np.atleast_2d(B).astype(int)
eq = (B[:, None, :] == B[None, :, :]).astype(float) # (n,n,p)
smc = np.mean(eq, axis=2) # (a+d)/p
return 1.0 - smc # distance
D_bin = pairwise_smc_distance(bin_points)
# 검증 (Hamming = (b+c)/p = 1 - (a+d)/p)
D_bin_sp = distance.squareform(distance.pdist(bin_points, metric='hamming'))
print("binary (SMC) allclose:", np.allclose(D_bin, D_bin_sp))
D_bin[:3, :3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# czekanowski
import numpy as np
def pairwise_czekanowski(P):
P = np.atleast_2d(P)
X = P[:, None, :] # (n,1,p)
Y = P[None, :, :] # (1,n,p)
num = 2.0 * np.sum(np.minimum(X, Y), axis=2)
den = np.sum(X + Y, axis=2)
S = np.divide(num, den, out=np.zeros_like(num), where=(den != 0))
return 1.0 - S
# 테스트용: 비음수 데이터로 변환하여 사용(예: 절댓값)
nonneg_points = np.abs(points.copy())
D_cz = pairwise_czekanowski(nonneg_points)
# 자체 성질 체크
print("czekanowski symmetric:", np.allclose(D_cz, D_cz.T))
print("czekanowski zero diag:", np.allclose(np.diag(D_cz), 0.0))
D_cz[:3, :3]
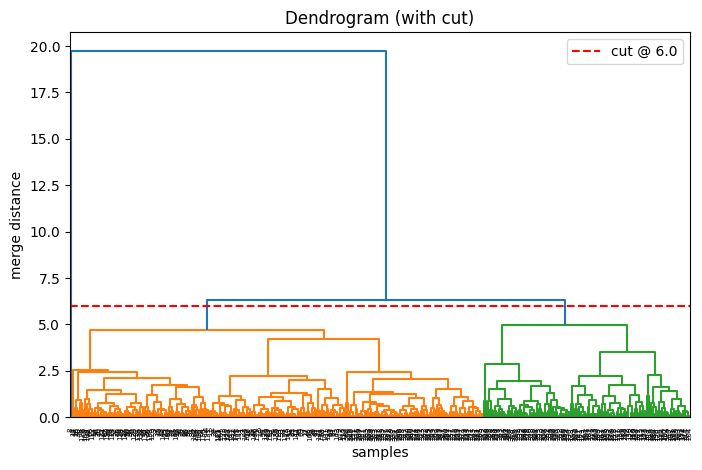
계층적 클러스터링
종류
- Agglomerative(bottom-up) : 모든 데이터 포인트가 독립된 클러스터로 시작하여 가장 가까운 두 클러스터를 합쳐간다. 최종적으로 하나가 될 때 까지 반복한다
- 모든 점을 독립된 n개의 클러스터로 시작(데이터 수 만큼 클러스터)
- 현재 클러스터 집합에서 가장 가까운 두 집합(A, B)의 linkage를 찾음
- A와 B집합을 합침
- 클러스터가 특정 threshold 혹은 1이 될때까지 반복
- Divisve(top-down) : 모든 점을 하나의 클러스터로 시작하여 계속 쪼개간다.
Linkage(거리)
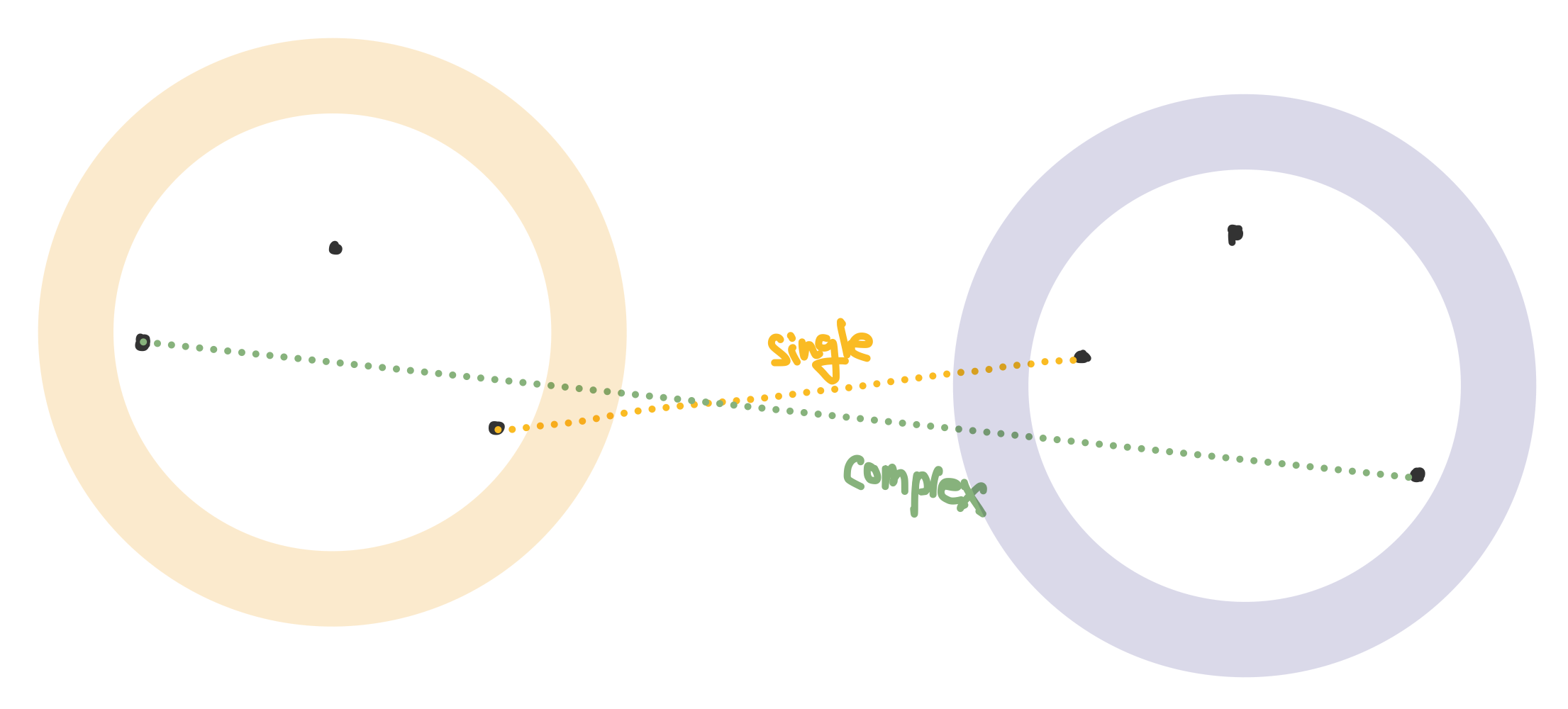
Single linkage : 두 클러스터안의 데이터 포인트에 대하여 가장 가까운 거리
complete linkage : 두 클러스터안의 데이터 포인트에 대하여 가장 먼 거리
average linkage : 두 클러스터 간 평균 거리